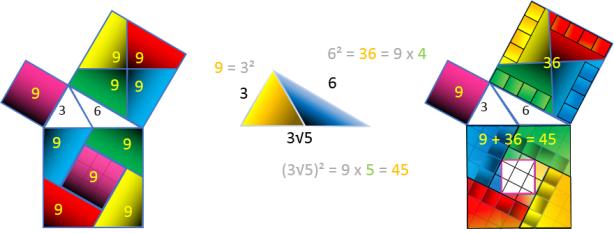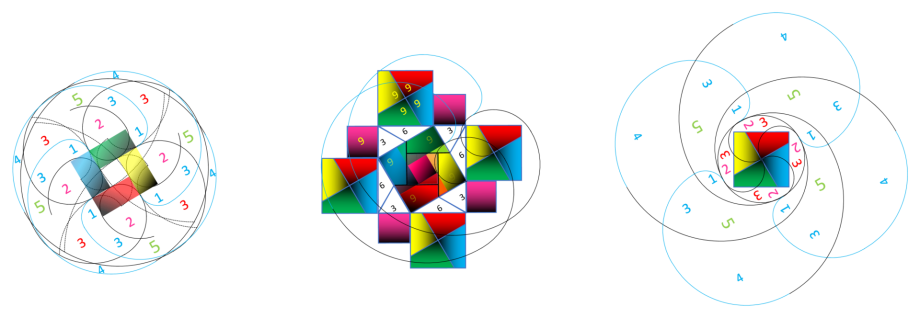Or Extra 4
Vous êtes peut être entrain de clôturer cette série du Calcul d'Or
Extra, mais en réalité l'aventure ne fait que commencer.
A votre avis, il y a quoi de plus fascinant que la lumière dans l'univers ?
L'obscurité ?
Il se trouve que la loi en Carrée Inverse, représente la frontière
entre ces deux états complémentaires. Elle est la base de la Physique Classique, elle a était dressée au départ par Isaac Newton, puis courbée par la relativité d'Albert
Einstein.
Dans la dernière partie du Calcul d'Or Extra, vous allez devoir rendre à cette loi en Carrée
Inverse son Carré d'Or, pour qu'elle vous délivre l'obscurité cachée sous la lumière.
Vous allez assistez à un cours dans une des plus grandes écoles de l'histoire, l'école
Pythagoricienne, fondée par un vrai connaisseur des nombres, Pythagore avec sa formule magique, vous délivrera un Carré de Rêve, ce rêve de pouvoir peut être un jour répondre à la question : à
quoi pouvaient servir toutes ces pyramides ?
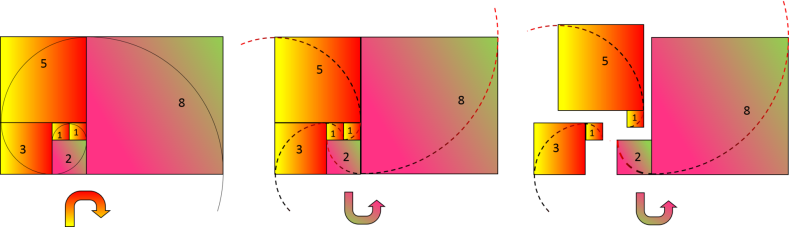
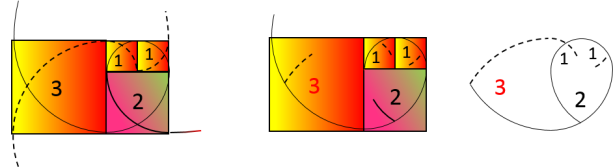
Le Rectangle de Fibonacci contient deux types de spirales de sens opposés :
-
Spirale d'Or : l'unique spirale qui tends vers le nombre d'Or en passant par tous les
carrés de Fibonacci.
-
Spirales Zohour : trois spirales dans le sens opposé de la spirale d'Or. Chaque spirale
passe par un tiers des carrés de Fibonacci pour tendre vers le nombre : (√5-1) = 1.2360679775
Les trois spirales Zohour forment des arcs brisés en coupant la spirale d'Or. Mais une seule spirale
de ces trois, apparaît comme une prolongation de la spirale d'Or dans son sens opposé. Cette dernière passe par tous les carrés de nombres pairs.
La décomposition en Rectangle Zohour fait apparaître cette spirale constituée uniquement de nombres pairs
:
 Rectangle Zohour
Rectangle Zohour
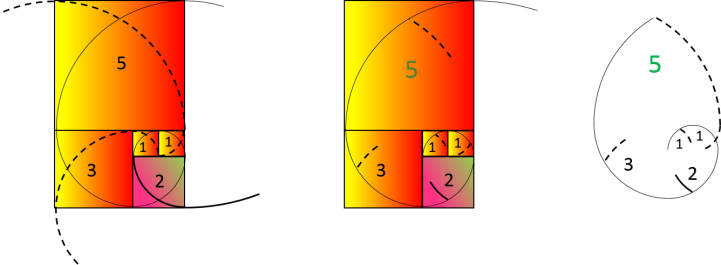
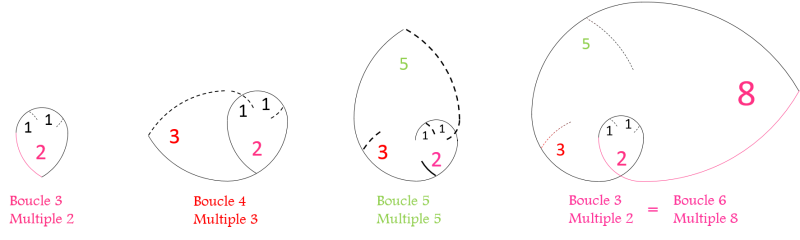
Cette spirale de nombres pairs, met en évidence la présence d'une boucle de 3 termes, représentant les
multiples de 2.
 Boucle 3 Multiple 2
Boucle 3 Multiple 2
La Boucle 3 Multiple 2 contient une boucle de 5 termes représentant les multiples de 5 :
 Boucle 5 Multiple 5
Boucle 5 Multiple 5
A l'intérieur de cette Boucle 5 multiple 5, on trouve une boucle de 3 termes représentant les multiples de
3 :
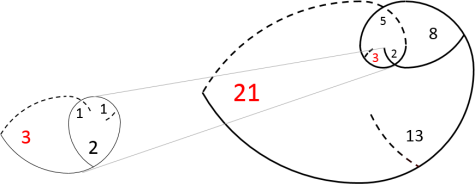 Boucle 4 Multiple 3
Boucle 4 Multiple 3
En suite, ce sont toujours les mêmes boucles qui se répètent à l'intérieur de la boucle 3 Multiple 2
:
 Pétales Zohour
Pétales Zohour
Toutes les boucles ci-dessus sont dynamiques, chacune donne naissance à une nouvelle boucle deux fois plus
grande représentant les multiples du dernier terme de la boucle précédente :
-
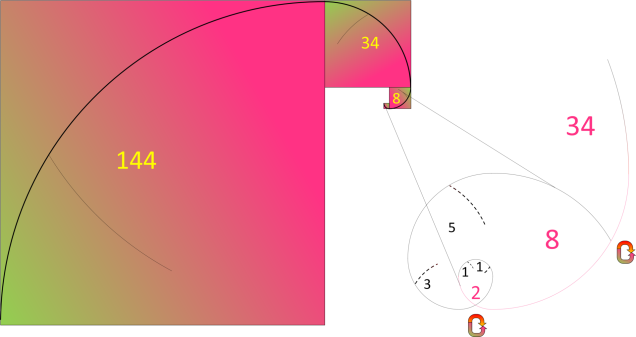
Boucle 3 Multiple 2 / Boucle 6 Multiple 8 : 144 = 18
x 8
-
Boucle 4 Multiple 3 / Boucle 8 Multiple 21 : 987 = 47 x
21
-
Boucle 5 Multiple 5 / Boucle 10 Multiple 55 : 6765 = 123 x 55
Il faut noter qu'une boucle Multiple N est aussi multiple des facteurs premiers de
N :
-
Boucle 3 Multiple 2 / Boucle 6 Multiple 4 : 8 = 2
x 4
-
Boucle 4 Multiple 3 / Boucle 8 Multiple 7 : 21 = 3 x
7
-
Boucle 5 Multiple 5 / Boucle 10 Multiple 11 : 55 = 5 x
11
On remarque que toutes les boucles supérieures sont des multiples des nombres d'Or Extra
(2,1,3,4,7,11,18,29,47,76,123,...), tout en restant des multiples des nombres de Fibonacci :
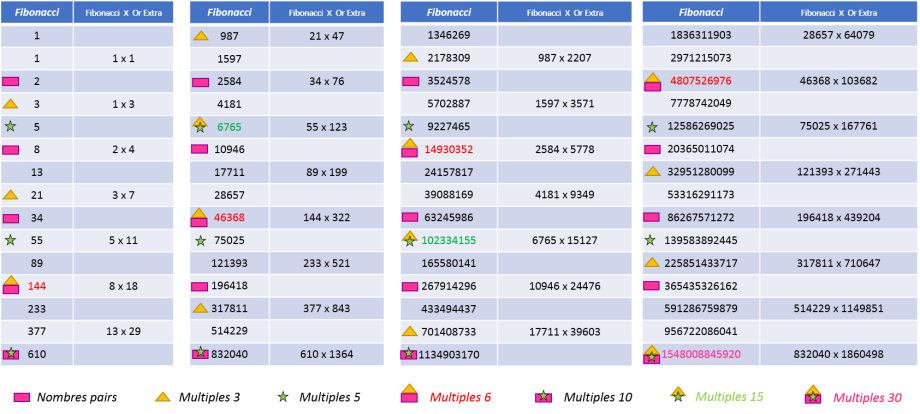 Boucle 60 Multiple 30 - Table de Fibonacci
Boucle 60 Multiple 30 - Table de Fibonacci
Nombreux sont ceux qui ignorent cette boucle de 60 termes de la suite de Fibonacci. Elle est pourtant
fortement liée au nombre d'or et aux nombres entiers. La table de Fibonacci ci-dessus, représente cette boucle qui se répète pour la simple raison que le 59ième terme se termine par
un 1 et le 60ième terme par un zéro, ce qui impose aux deux termes suivants de se terminer par un 1, tout comme au commencement de la suite de Fibonacci:
-
Premier terme : 1 + 0 = 1 →
59ième + 60ième = 61ième
-
Deuxième terme : 0 + 1 = 1 → 60ième + 61ième = 62ième
Il faut noter que le même phénomène se reproduit qutre fois à l'intérieur de cette boucle de 60 termes sur
une période de 15 :
-
Seizième terme : 377 + 610 = 987
-
Dixseptième terme : 610 + 987 = 1597
Il suffit d'observer les deux premières lignes de cette table pour voir la double présence des chiffres :
1, 7, 9, et 3. Ces chiffres correspondent à des nombres impairs, dans une boucle répartie en quatre parties. Il est donc préférable de travailler avec des chiffres pairs qui sont au nombre de
quatre (2,4,6,8), qu'avec des chiffres impairs qui sont au nombre de cinq (1,3,5,7,9).
Il n'est pas nécessaire de tout multiplier par 2 pour travailler uniquement avec des nombres paire. Car il
suffit de prendre la troisième ligne pour faire apparaître cette boucle des chiffres pairs (2,4,8,6) qui correspond aussi au double de la boucle (1,7,9,3).
Toutes les lignes contenants des nombres pairs suivent la même boucle, à l'exception de la dernière ligne
qui contient les multiples de 10 :
-
Troisième ligne : (2,4,8,6) avec 6 représentant un multiple de 6.
-
Sixième ligne : (8,6,2,4) avec 2 représentant un multiple de 6.
-
Neuvième ligne : (4,8,6,2)
avec 8 représentant un multiple de 6.
-
Douzième ligne : (4,8,6,2) avec 4 représentant un multiple de 6.
-
quinzième ligne : (2,8,4,4) avec 4 représentant un multiple de 6.
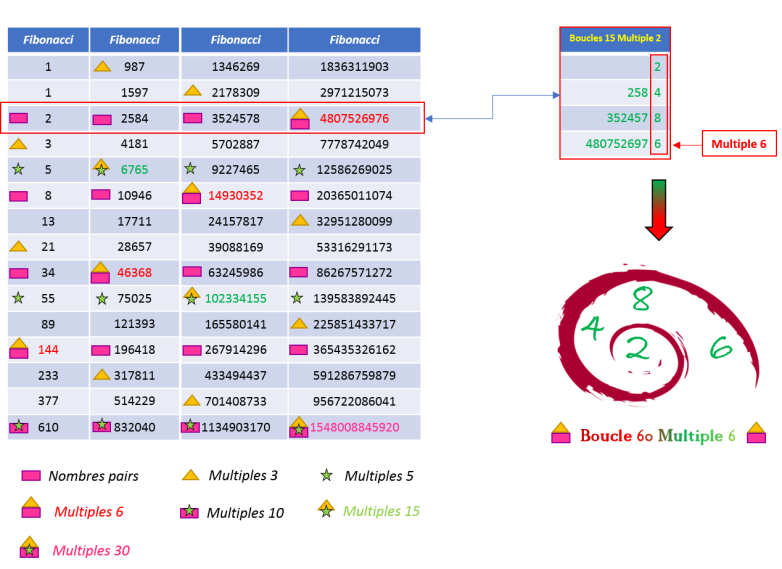 Boucle 60 Multiple 6 - Table de Fibonacci
Boucle 60 Multiple 6 - Table de Fibonacci
La quinzième et dernière ligne correspond aux multiples de 5 tout en étant des nombres pairs, d'où la présence du zéro. Elle est aussi conforme à la période d'apparition des multiples
de 6 en se terminant par un multiple de 30 (5x6=30). Mais la boucle est différente. Elle est la même que celle des quatre premiers nombres pairs de la suite de Fibonacci :
-
(2,8,34,144) pour une boucle
(2,8,4,4) avec 4 représentant un multiple de 6.
En réalité, il se produit le même phénomène que celui rencontré au départ avec la double présence des
chiffres impairs dans les deux premières lignes :
-
Les quatre premiers termes (1,1,2,3) multipliés par 4, suivent une boucle (4,4,8,2) avec 2 représentant
un multiple de 6.
Ainsi la boucle (2,8,4,4) correspondant à la dernière ligne, et aux quatre premiers nombres pairs (2,8,34,144), semble être la boucle inverse des quatre premiers termes (1,1,2,3) avec la boucle (4,4,8,2). Or cette boucle et son inverse n'existent qu'à travers une
boucle de 5 termes :
-
(2,8,4,4,0) : avec
(2,8,34,144,610).
-
(4,4,8,2,0) : avec (1,1,2,3,5).
Difficile de
travailler avec des chiffres pairs sur cette boucle de 5 termes, avec l'apparition du zéro et la double apparition des chiffres pairs. Les chiffres impairs qui sont au nombre de 5, s'adaptent mieux à
cette boucle InFernal (Calcul InFernal).
La table d'Or Extra ci-dessous, est nécessaire pour le passage des nombres de Fibonacci au nombre d'or, et
ainsi accéder à tous les nombres d'Or Parfaits vus au chapitre 3 (Rectangle d'Or Parfait).
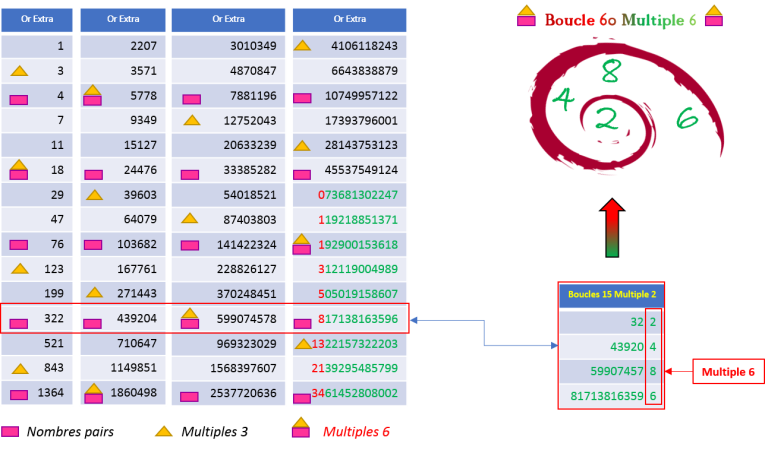 Boucle 60 Multiple 6 - Table d'Or Extra
Boucle 60 Multiple 6 - Table d'Or Extra
Toutes les lignes de cette table font apparaître la même boucle (2,4,8,6). Il suffit de tout multiplier par
2 pour que les nombres impairs s'y retrouvent aussi.
En ce qui concerne les lignes contenants les nombres pairs, on retrouve la même période d'apparition des
multiples de 6 :
-
Troisième ligne : (4,8,6,2) avec 8 représentant un multiple de 6.
-
Sixième ligne : (8,6,2,4) avec 8 représentant un multiple de 6.
-
Neuvième ligne : (6,2,4,8) avec 8 représentant un multiple de 6.
-
Douzième ligne : (2,4,8,6) avec 8 représentant un multiple de 6.
-
quinzième ligne :
(4,8,6,2) avec 8 représentant un multiple de 6.
En réorganisant la répartition des nombres d'Or Extra sous forme de 5 parties, on retrouve les boucles
InFernal composées de 5 chiffres sur les 4 lignes de nombres pairs de la table ci-dessous :
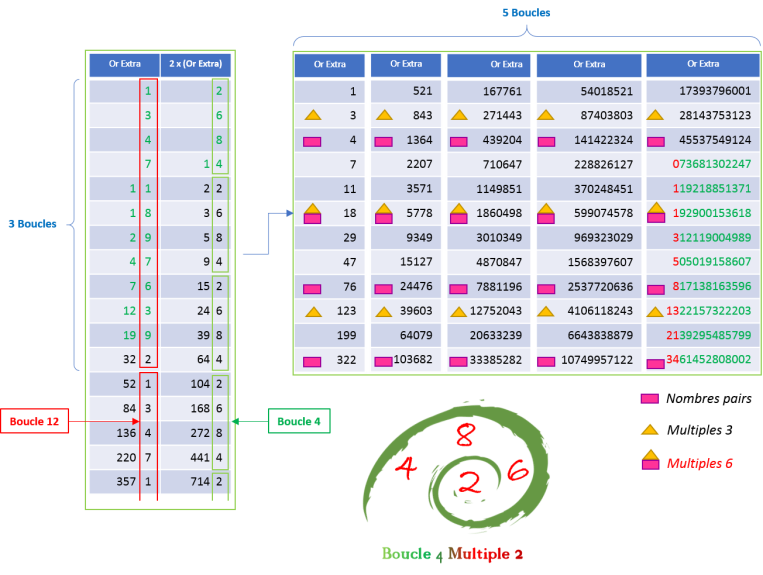 Boucle 4 Multiple 2 - Or Extra
Boucle 4 Multiple 2 - Or Extra
Ces lignes de nombres pairs montrent la présence multiple des mêmes chiffres pairs :
-
Troisième ligne : (4,4,4,4,4)
-
Sixième ligne : (8,8,8,8,8)
-
Neuvième ligne : (6,6,6,6,6)
-
Douzième ligne : (2,2,2,2,2)
Chaque chiffre des boucles ci-dessus représente une boucle de 12 termes :
-
Première colonne : (4,8,6,2) avec (4,18,76,322).
En multipliant par deux tous les nombres d'Or Extra, on s'aperçoit qu'il y a encore une boucle plus petite
(2,6,8,4) "Boucle 4 Multiple 2 ", présente 3 fois de suite pour former la boucle (4,8,6,2) qui est sa boucle inverse (Calcul InFernal).
Pour la suite nous allons nous intéresser uniquement à la boucle (2,4,8,6) contenant un multiple de 6
présente dans les deux tables Or Extra et Fibonacci. Car le chiffre 6 est étroitement lié à l'espace temps et à la loi en carré inverse.
Cette boucle d'Or Extra (2,4,8,6) est remarquable, car elle forme un arrangement numérique de dimension
1000, comme le montre le tableau ci-dessous avec les deux boucles Or Extra et Fibonacci exprimées en millimètre :
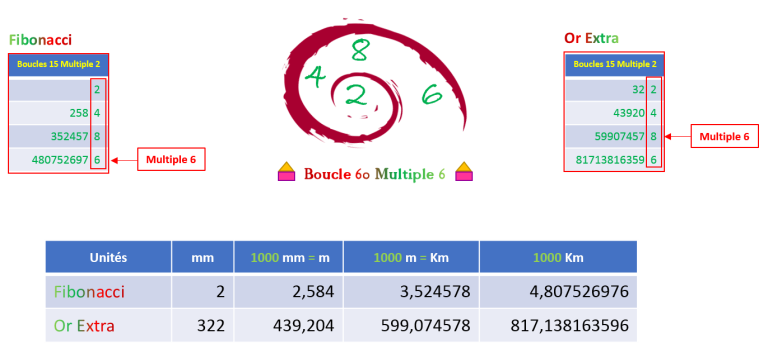 Dimension d'Or - 1000
Dimension d'Or - 1000
Cette Dimension d'Or est nécessaire pour le passage d'un calcul scientifique utilisant le système décimale
à un Calcul d'Or Extra utilisant le nombre d'or. Elle permet de choisir les nombres d'or les mieux adaptés à chaque situation en terme d'espace et d'espace temps. Car elle couvre les quatre
chiffres de la boucle sur une période de 60 (Boucle de 60 termes), tout comme une montre le fait pour une boucle d'une heure avec 60 minutes.
Le chapitre 1 du Calcul d'Or Extra, montre que toute distance peut être exprimée avec la même boucle
que celle utilisée par l'espace temps :
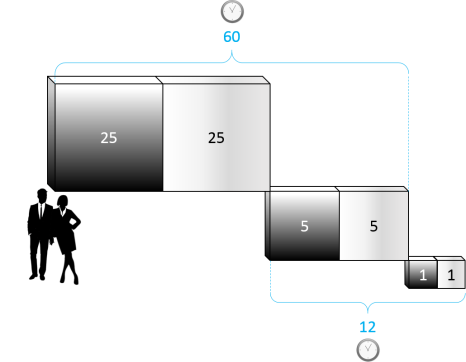 Boucle Or Extra 2468 - Chapitre 1
Boucle Or Extra 2468 - Chapitre 1
Car une montre, tout comme le Calcul d'Or Extra considère que :
-
Le chiffre Zéro n'existe pas : 00=24
-
Le chiffre 2 est la base pour toute mesure : 2 x 12 = 24 = 00
-
Le chiffre 6 est l'union du couple : 60s, 60 min, 24h.
Cette montre contenant des multiples de 6 qu'on utilise tous les jours pour se repérer dans l'espace temps,
est le reflet du mouvement relatif existant entre la Terre et le Soleil. Ce mouvement est fortement lié au chiffre 6 et aux variations saisonnières sur Terre (Manuel d'Eau et de
Ciel).
Il n'est pas surprenant que les chiffres indo-arabes s'arrêtent au chiffre 9, qui possède le même symbole
que le chiffre 6, mais avec une orientation inverse. Cette relation entre le 6 qui est pair, et le 9 qui est impair, apparaît comme la base de l'invention des chiffres indo-arabes. Ce n'est qu'en
étudiant le comportement de la lumière à travers la loi en carré inverse, qu'on peut comprendre pourquoi ces chiffres s'arrêtent au chiffre 9.
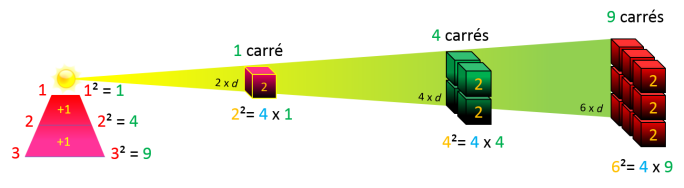
Pour un physicien, l'intensité de la lumière est inversement proportionnelle au carré de la distance de son
origine. Ce qui revient à dire qu'une quantité de lumière venant d'une source lumineuse, reste constante durant sa progression à travers des surfaces proportionnelles aux
distances.
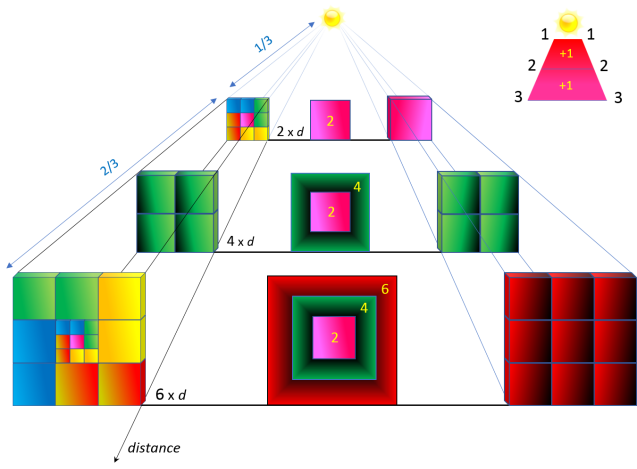 Loi en carré inverse
Loi en carré inverse
On dit qu'une loi est en carré inverse, pour les raisons suivantes :
-
Carré : les distances parcourues par la lumière, restent proportionnelles aux surfaces éclairées par cette
même quantité de lumière. Or une surface n'est que le carré d'une distance.
-
Inverse : l'intensité de la lumière diminue quand la distance augmente. Car nous avons toujours
la même quantité de lumière pour des surfaces de plus en plus larges.
Si une quantité de lumière éclaire une surface de 2² à une distance 2xd, alors elle va certainement
éclairer une surface de 4² à une distance 4xd, et une autre de 62 à une distance 6xd et ainsi de suite :
Travailler avec des nombres pairs ou des nombres impairs ne change en rien le résultat final. Il suffit de
transformer le 9 en un 6 (9x4=36) pour passer des nombres impairs aux nombres pairs. Ainsi toutes les distances simples se transforment en des distances doubles.
Ce phénomène se reproduit entre le premier carré au nombre de 1 et le dernier carré au nombre de 9,
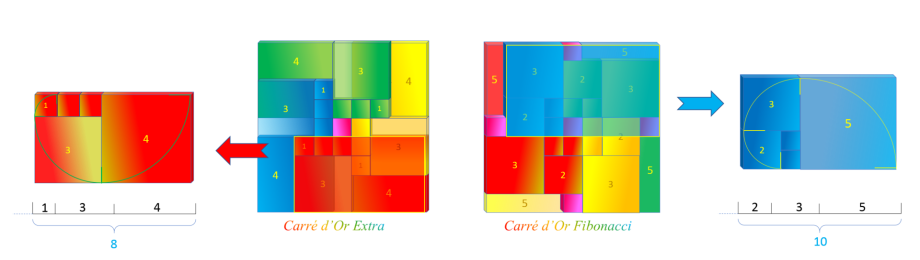
exactement comme le fait le Carré d'Or :
 Carré d'Or
Carré d'Or
Le Carré d'Or offre la possibilité d'avoir un arrangement géométrique faisant apparaître les nombres de
Fibonacci et les nombres d'Or Extra. Ce qui rend facile l'introduction du nombre d'or dans cette loi si importante dans notre univers :
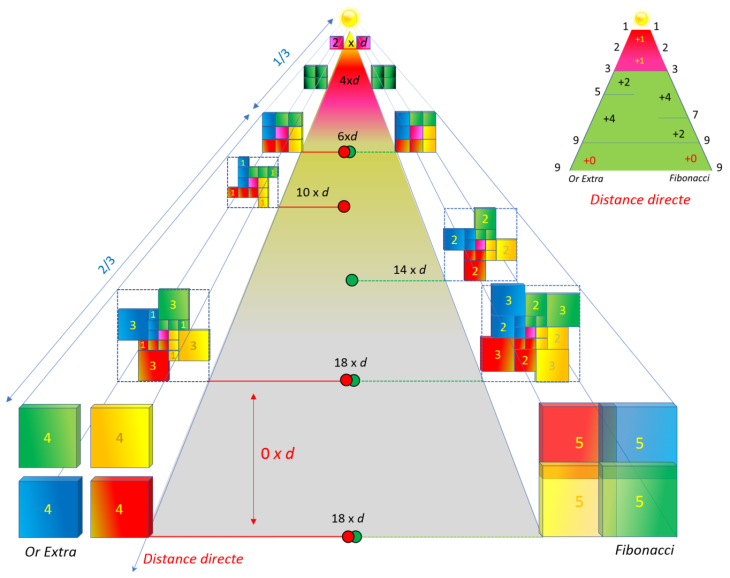 Loi en Carré d'Or - Distances directes
Loi en Carré d'Or - Distances directes
Là où certains scientifiques voient un zéro, d'autres se perdront dans une infinité de probabilités
quantiques.
Dans cette zone zéro, il se passe un phénomène nécessaire à la vision humaine, que l'on appelle la
réflexion en optique. Sans ce reflet on ne peut expliquer le fait de voir un objet éclairé par une lumière.
Il faut toujours garder à l'esprit, que ce qui est nécessaire n'est pas
forcement suffisant. On ne peut parler de vision humaine sans évoquer le père de l'optique moderne Ibn al-Haytham et la Camera Obscura qui fait le bonheur de tous les amateurs de la
photographie.
Tout objet éclairé n'est visible que si son reflet passe par un petit
trou menant dans une chambre noire. D'où l'importance de l'obscurité et l'infiniment petit.
La lumière visible est constituée d'un ensemble d'ondes électromagnétiques perçues par la vision
humaine.
Ces ondes peuvent êtres modélisées par des spirales, mais pour la suite de ce chapitre, les deux spirales
utilisées ne sont que des repères imaginaires.
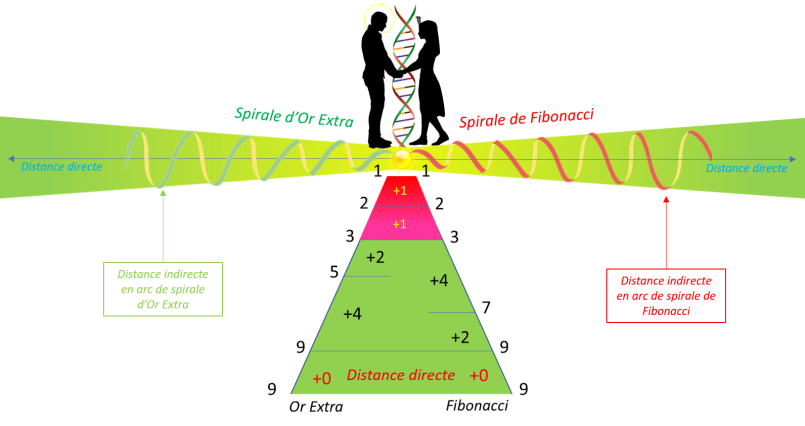
Ces deux spirales repères, forment une extension des distances directes
réelles. On retrouve le même principe en mathématique avec les nombres complexes qui offrent une extension des nombres réels grâce à un nombre imaginaire i tel que i2=-1 (Calcul InFernal).
Chacune des deux spirales Or Extra et Fibonacci, permet d'introduire un
nouveau paramètre nommé "Distance Lumière", qui correspond à la distance indirecte parcoure par la lumière en suivant un arc de spirale :
Cette Lumière en spirale reste scientifiquement impossible, car cela signifie qu'elle se déplace plus vite
que la vitesse de la lumière. En effet, il faut aller beaucoup plus vite sur une distance indirecte que sur une distance directe, si l'on veut arriver en même temps.
Rappelons que les deux spirales Or Extra et Fibonacci sont deux suites d'entiers qui tendent vers le nombre
d'or, et qui correspondent à la somme des deux termes précédents. Donc la longueur d'arc dans la zone zéro, correspond à la somme des deux arcs précédents :
-
Or Extra : 12 x a = (4 x a) + (8 x a) ; avec a unité
d'arc quelconque.
-
Fibonacci : 12 x a = (8 x a) + (4 x a) ; avec a unité d'arc
quelconque.
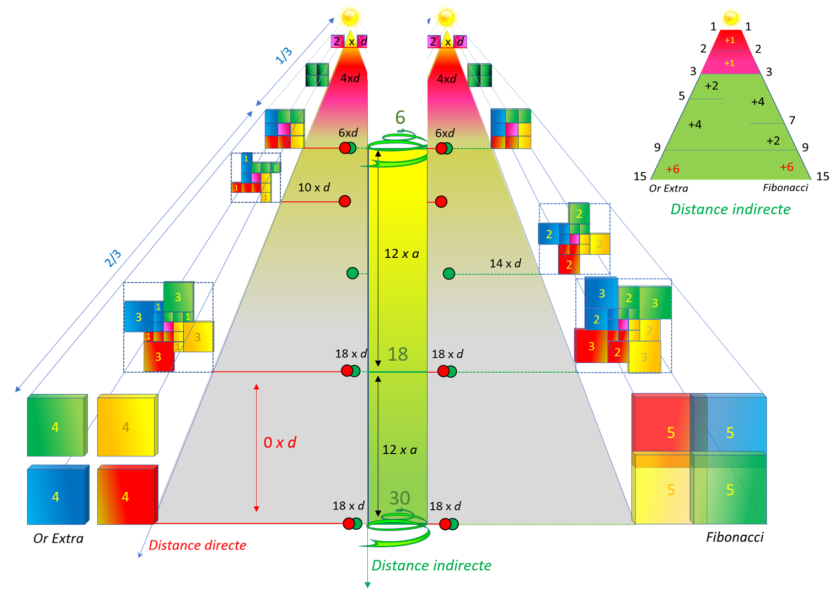 Loi en Carré d'Or - Distance Lumière : Distances indirectes en arc
Loi en Carré d'Or - Distance Lumière : Distances indirectes en arc
Pour garder un lien entre les distances directes et les distances indirectes, on suppose qu'il existe une
unité d'arc a proportionnelle à l'unité de distance d
. Ainsi les longueurs d'arcs des deux spirales Or Extra et Fibonacci sont proportionnelles aux distances directes.
Cette unité d'arc a varie
d'une spirale à l'autre :
 Longueur d'arc Or Extra & Fibonacci
Longueur d'arc Or Extra & Fibonacci
L'unité d'arc doit être proportionnelle à la longueur d'arc :
-
Or Extra : longueur d'arc = 8 = 2 x
4
-
Fibonacci : longueur d'arc = 10 = 2 x 5
La spirale d'Or extra exige une
unité d'arc multiple de 4, or la spirale de Fibonacci exige une unité d'arc multiple de 5.
Sans surprise, la longueur d'arc des deux spirales est un multiple de 9 :
-
Longueur d'arc totale = 18 = 2 x 9
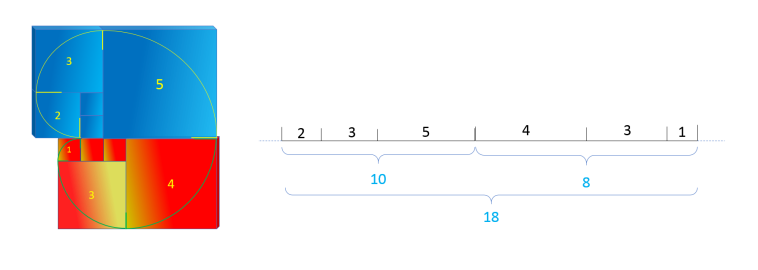 Pomme d'Or - Longueur totale d'arc Or Extra & Fibonacci
Pomme d'Or - Longueur totale d'arc Or Extra & Fibonacci
La Pomme d'Or ci-dessus fait apparaître une boucle fermée, avec une continuité entre la spirale d'Or
Extra et celle de Fibonacci au passage du 4 au 5 d'où le terme boucle. Cette boucle se referme sur elle même entre le 2 et le 1 ce qui correspond plutôt à un nœud d'où le terme fermée (Calcul InFernal).
Tout ce qui se cache à l'intérieur ou derrière quelque chose est InFernal. Comme par exemple les deux
premiers termes de Fibonacci égales à 1 :
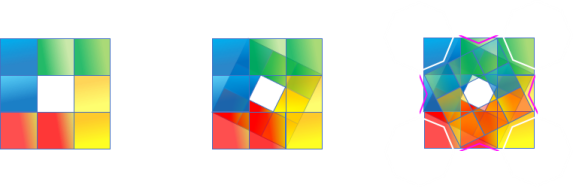
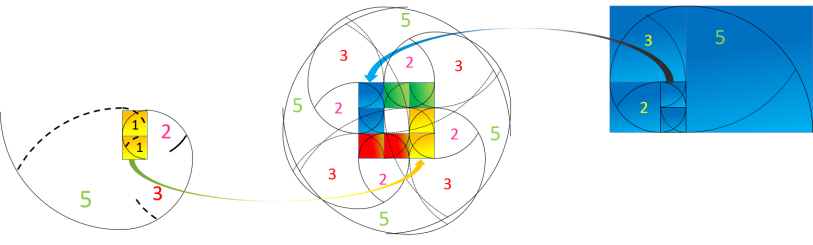 Carré d'Or en Pétales Zohour
Carré d'Or en Pétales Zohour
On peut aussi considérer l'arc brisé correspondant à 5 comme infernal, car il est le seul à traverser le
carré d'or et former avec les autres arcs de 5 un carré d'arcs interne :
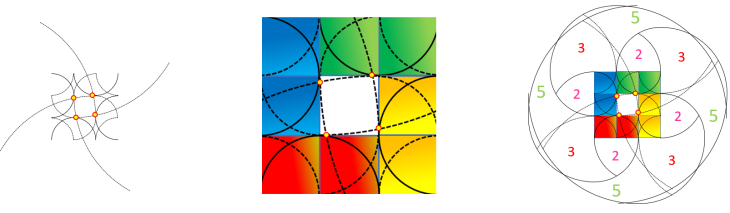 Carré d'arcs interne
Carré d'arcs interne
La Calcul d'Or Extra correspond au reflet externe des choses, dans un espace où tout est pair, ainsi les
nombres impairs restent invisibles, car ils se retrouvent toujours entourés de nombres pairs ce qui les rends eux-mêmes pairs :
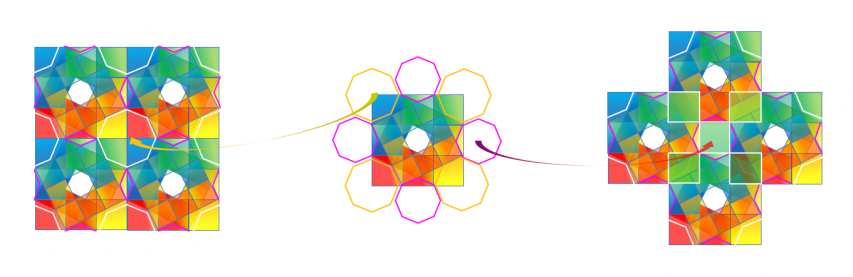
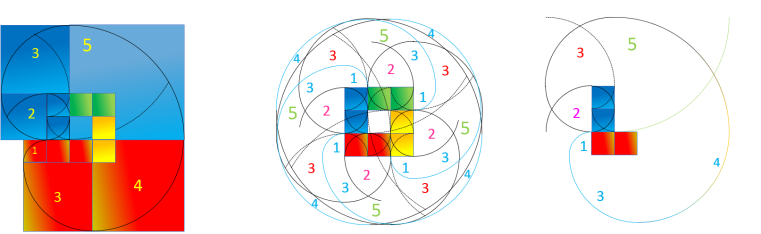 Boucle d'Or
Boucle d'Or
En observant cette boucle d'Or de l'extérieur à l'intérieur, on s'aperçoit que le chiffre 4 entoure le
chiffre 5 et tous les autres chiffres, ce qui rend le 5 InFernal et le 4 Or Extra.
Il faut noter que l'arc brisé de Fibonacci du chiffre 2 entoure les chiffres 1 et 3 de la spirale d'Or
Extra, et que cet arc brisé est l'unique spirale constituée uniquement de nombres pairs (Rectangle Zohour).
Maintenant que nous savons le comportement des spirales Or Extra et Fibonacci à l'extérieur du Carré d'Or,
nous allons voir ce qui s'y cache à l'intérieur :
Il suffit de souligner toutes les diagonales (au nombre de 8) pour faire apparaitre les deux Carrés d'Or
cachés à l'intérieur du premier. A ne pas confondre avec une étoile à huit branches, car ces deux carrés internes font le lien entre deux octogones réguliers de tailles différentes, comme le montre
les deux pavages ci-dessous :
On constate que le pavage de droite présente des interférences, contrairement à celui de gauche qui
correspond à un assemblage parfait. En réalité, même à l'intérieur du Carré d'Or on retrouve cette frontière entre le chiffre 4 et le chiffre 5 :
Cette frontière séparant les pairs des impairs, tire ses racines des nombres irrationnels cachés sous les
diagonales du Carré d'Or de base :
L'image ci-dessus montre qu'en changeant de repère et d'unité de mesure, un nombre irrationnel peut devenir
un nombre entier.
Cette transformation est nécessaire pour pouvoir utiliser la formule de Pythagore :
La formule de Pythagore correspond à une opération de soustraction, ce qui nous sera très utile pour
comprendre comment une pyramide peut soustraire la lumière du Soleil :
Une pyramide, ou tout autre objet n'est visible qu'à travers son reflet. Or, là où il y a un reflet il y a
une ombre. Ce sont ces deux états opposés et complémentaires qui constitue la lumière.
Ce couple de lumière (Reflet , Ombre) n'est que le couple d'Or (Or Extra
, Fibonacci) :
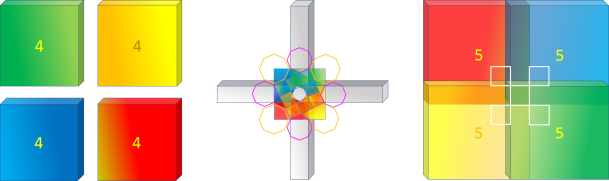
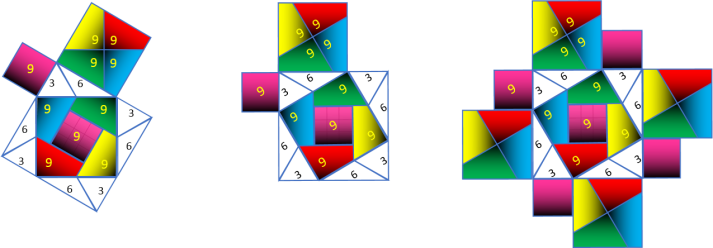 Carré de Rêve
Carré de Rêve
Le Carré de Rêve est un Carré d'Or contenant un autre de sens opposé :
 Carré de Rêve
Carré de Rêve
Ce qui permet d'observer le comportement des spirales Or Extra et Fibonacci pendant cette opération de
soustraction :
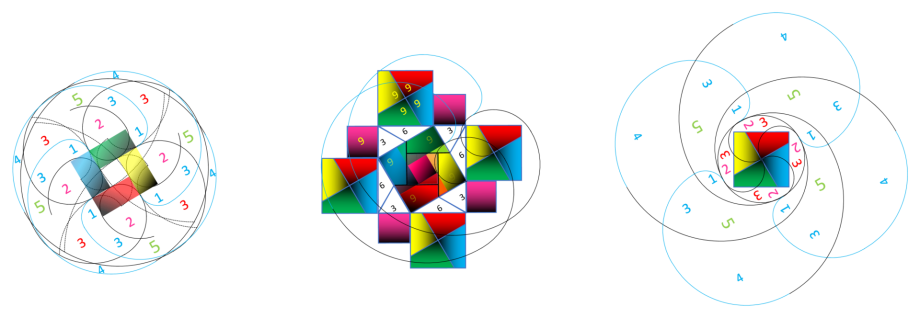 Fleur d'Or Extra 4
Fleur d'Or Extra 4
Avec cette fleur à quatre pétales s'achève le Calcul d'Or Extra et notre quête des chiffres pairs, pour
laisser la main au Calcul InFernal, un calcul à base de cinq chiffres impairs.