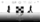Or Extra 1
Dans cette Première Partie du Calcul d'Or Extra, vous allez vous
attaquer au pilier de tout calcul scientifique, le zéro. Ce chiffre est tout simplement la frontière entre le savoir de notre
civilisation actuelle est le savoir perdu des anciennes civilisations.
Imaginez-vous un chiffre qui représente rien, seulement du vide absolu, et pourtant on lui réserve
une place dans tous les ordinateurs du monde entier. Il est juste indispensable pour toute mesure scientifique dans
l'espace-temps.
En réalité le zéro symbolise un point de départ, mais les symboles des chiffres s'arrêtent à 9,
alors on l'utilise pour marquer le début d'une nouvelle période avec le nombre 10, et ainsi de suite.
A partir de maintenant, vous allez devoir apprendre à vous séparer
du chiffre zéro, pour la simple et bonne raison : "Quand vous mesurez un objet, vous mesurez sa matière, alors que le zéro se situe là où il n'y a pas de matière".
" Tout est nombre. " c'est le grand apport de Pythagore, l'importance de la notion des nombres et le
développement d'une mathématique géométrique. Toutes les anciennes civilisations de l'antiquité considèrent les nombres comme des nombres entiers.
Il est vrai que l'homme de l'antiquité n'avait pas connaissance de la virgule pour utiliser des nombres
décimaux, mais cela ne signifie pas qu'il était incapable de construire avec une précision allant même jusqu'au nombres irrationnels.
Les mathématiques doivent leur existence à ce que l'on appel un système arrangé numériquement. De nombreux
systèmes ont été utilisés par des peuples et à des époques différentes.
Le système de numération indo-arabe est devenu aujourd'hui l'outil de base pour toute mesure scientifique.
Dans ce système à base de dix, on utilise dix chiffres allant de zéro à neuf, que l'on appellera par la suite la boucle indo-arabe.
 La boucle indo-arabe
La boucle indo-arabe
La boucle indo-arabe commence par le chiffre zéro, suivi par l'unité 1, pour se terminer avec le
nombre 10. Ce dernier devient le commencement de la boucle suivante. Comme pour une montre qui affiche l'heure de minuit; la fin d'une journée annonce le commencement d'une nouvelle, ainsi
l'heure 24:00 est la même que l'heure 00:00. Pour la boucle indo-arabe cela revient à dire que l'heure 10:00 et la même que l'heure 00:00.
En répétant dix fois de suite cette boucle, on obtient une nouvelle boucle dix fois plus grande, qui
commence par le 0 suivi par l'unité 10, pour se terminer avec le nombre 100.
L'unité 1, est elle aussi constituée de la même boucle, elle est donc forcement un multiple de 10, c'est le
cas quand vous mesurez une distance égale à 1cm, cela correspond aussi à 10mm.
Il faut noter que la boucle représente l'unité, ce qui signifie que l'unité est toujours un multiple de 10,
donc un nombre pair ( 10 = 2 x 5 ).
Sachant que l'unité est un nombre pair, on peut conclure que tous les nombres qui résultent du système
décimal sont donc des nombres pairs. Cela signifie qu'un scientifique, sans s'en rendre compte, n'utilise que des nombres pairs pour tout calcul utilisant le système décimal
indo-arabe.
En multipliant par 2 tous les nombres
(0,1,2,3,4,5,6,7,8,9...) on n'obtient que des nombres pairs (0,2,4,6,8,10,12,14,16,18,...). Ce qui permet de
passer d'une boucle de 10 avec (0,1,2,3,4,5,6,7,8,9) à une boucle de 5 avec (0,2,4,6,8).
Cette boucle indo-arabe réduite à 5, commence par le 0 suivi par l'unité 2 pour se terminer avec le nombre
10 :
 Boucle indo-arabe réduite à 5
Boucle indo-arabe réduite à 5
Toutes les boucles ci-dessus commencent ou se terminent par un nombre utilisant le chiffre zéro
(0,10,20,30,40,...). Ces nombres sont tous des multiples de 2, 4, 6 ou 8, alors il y a forcement une boucle (2,4,6,8), capable de représenter tout les nombres pairs.
A partir de ce stade le chiffre zéro n'a plus aucune importance, il suffit de le considérer comme
inexistant, pour obtenir une boucle Or Extra, une boucle à base de 4 chiffres, qui commence par l'unité 2, et se termine par l'unité suivante 2x5.
 Boucles Or Extra 2468
Boucles Or Extra 2468
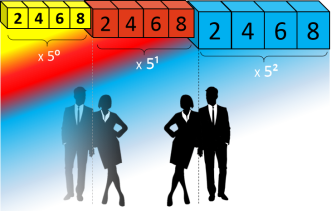
En répétant 5 fois de suite cette boucle, on obtient la boucle supérieure qui est 5 fois plus grande que la
boucle de base.
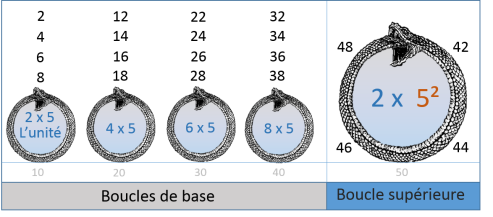 Boucles de base suivies d'une boucle supérieure
Boucles de base suivies d'une boucle supérieure
Il faut noter que l'unité est toujours un multiple de 5, et que ce chiffre est lié au
chiffre 6 par la relation suivante : (1+5)=6.
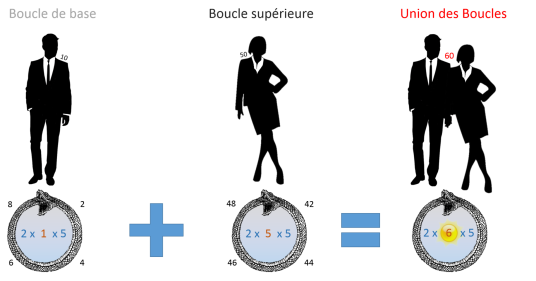 Union d'une boucle de base avec sa boucle spérieure
Union d'une boucle de base avec sa boucle spérieure
Cet arrangement numérique (2, 4, 6, 8), est le reflet du système décimal dans un espace où tous les
nombres sont pairs. Ainsi les nombres impairs sont invisibles, car ils sont toujours entourés de nombres pairs, ce qui les rends eux-mêmes pairs.
 Règle d'Or Extra 1
Règle d'Or Extra 1
Ainsi, avec uniquement des nombres pairs, on peut reconstituer tous les nombres entiers (pairs et
impairs) du système décimal.
Contrairement à un calcul scientifique qui utilise une unité de mesure égale à 1, le Calcul d'Or Extra
utilise une unité de mesure égale à ½ pour pouvoir travailler uniquement avec des nombres pairs.
-
Unité de mesure = ½
(tous les nombres sont pairs)
Avec l'unité égale à ½, tous
les nombres (0,1,2,3,4,5,6,7,8,9,...) deviennent des nombres pairs (2,4,6,8,10,12,14,16,18,...).
Comme évoqué précédemment, les nombres pairs ne sont en réalité qu'un seul
et unique couple (Homme,Femme) qui se répète jusqu'à l'infini.
Ce couple (H,F) est lié à jamais par l'unité du couple
UC = (UH,UF). Homme et Femme ont chacun sa propre unité mais leurs somme est toujours un multiple de 6 (union des boucles), si l'Homme prend une unité
égale à 1, la Femme prendra une unité égale à 5, pour que la somme des deux soit égale
à 6.
Union du couple : (UH + UF)
= 6
Prenez la règle d'Or Extra 1 ci-contre, elle
représente le couple (H,F), avec l'Homme représentant les graduations de gauche et la femme celles de droite. Pour savoir à quelle hauteur s'est posé le
petit oiseau, il suffit d'identifier le couple (H,F) = ( 8 , 4 ), de prendre l'unité du couple (1 , 5 ), pour que la mesure soit : 8 x 1 + 4 x 5 = 28, sans
oublier de multiplier par l'unité de mesure (½) ce qui vous donne un total de 14.
-
Unité de mesure = ½
-
Couple ( H , F ) = ( 8 , 4 )
-
UC = ( UH , UF ) = ( 1 , 5 )
-
Mesure du couple = ( 8 x 1 + 4 x 5 ) x ½ = 14
La règle d'Or Extra n'a pas de dimension précise, sa longueur totale
LT est égale à 1, ce qui représente l'unité, et correspond à une seule graduation de 2, sans oublier l'unité de mesure
½ :
L'unité peut être n'importe quelle distance, elle varie en fonction de l'unité du couple choisie, tout en
restant toujours un multiple de 5 :
-
Unité = LT = 5
x UF = 25 x UH
Si la distance Terre/Soleil était égale à 27, avec l'unité du couple ( 1 , 5 ) la Terre se
placera en dehors de la règle :
-
UC = ( 1 , 5
)
-
LT = 5 x
UF = 25
-
Distance Terre/Soleil = 27
-
27 > 25 (Terre à l'extérieur de la règle)
 Règle d'Or Extra 1
Règle d'Or Extra 1
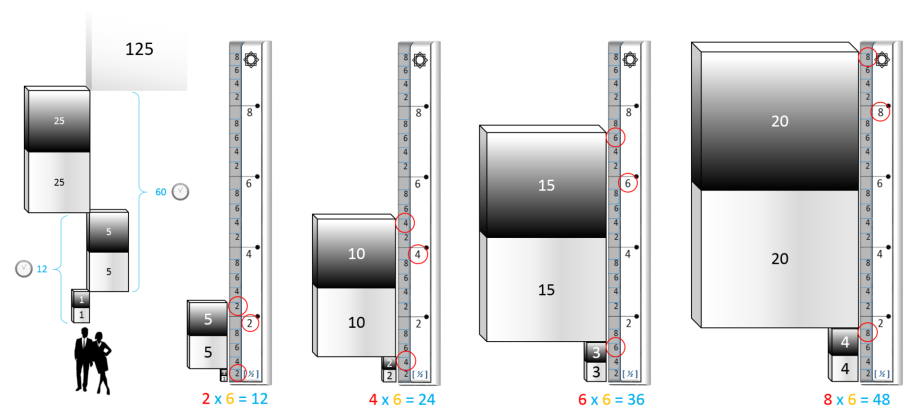
Avec l'unité du couple ( 5 , 5²) la Terre se placera au niveau du couple ( 2 , 2 )
:
-
Unité de mesure = ½
-
Couple ( H , F ) = ( 2 , 2 )
-
UC = ( UH , UF ) = ( 5 ,
5²)
-
LT = 5 x UF = 125 (Terre à l'intérieur de la règle car
125>27)
-
Mesure du couple = ( 2 x 5 + 2 x 5² ) x ½ = 30
-
Distance Terre/Soleil = 27
-
30 > 27 (Terre à l'intérieur de la règle).
En insérant une nouvelle règle d'Or Extra, vous augmentez la précision de la mesure, et ainsi de
suite jusqu'à la précision absolue.
En physique, toute mesure se doit de garder un lien entre l'espace et le temps. Sachant que le temps ne se
mesure pas en base de 10, et que la seconde est l'unité de mesure dans le système international, il devient nécessaire de travailler avec des multiples de 6 pour accéder aux unités supérieures comme
la minute (1 min = 60 s) ou le jour (1 j = 24 h ) :