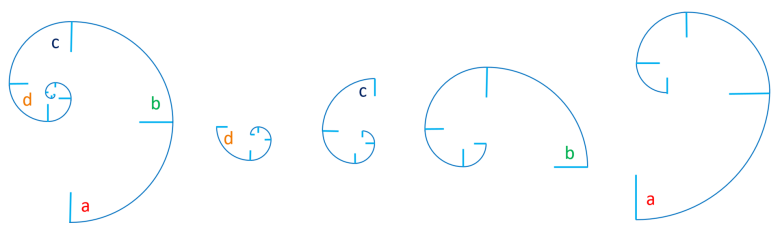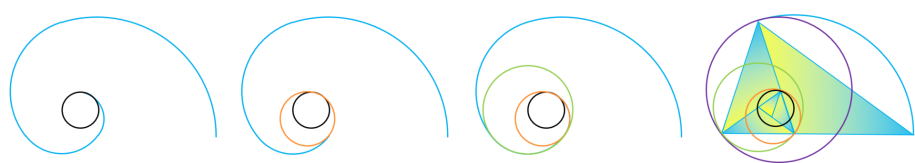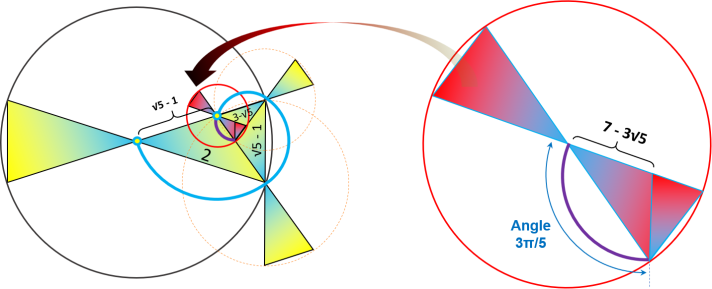InFernal 1
Ce qu'il y a d'intéressant en mathématiques, c'est qu'il n'y a ni bien ni mal, il n'y a que la
vérité. Mais aussi intéressante qu'elle puisse paraître, cette vérité reste la plupart du temps cachée derrière des nombres et des équations que seul l'inventeur détient le
secret.
Pour commencer ce livre, vous serez confrontés à une seule et unique vérité qui
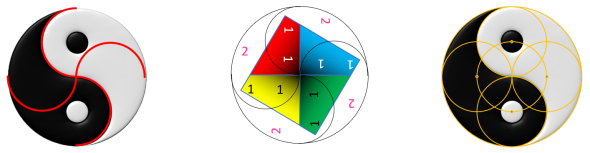
est " la différence ", cette différence que l'on retrouve dans la philosophie chinoise sous le nom " Yin et Yang ", et qui est aussi présente dans les chiffres indo-arabes sous forme de chiffres pairs et chiffres impairs.
Avant de plonger dans cet univers, il va falloir le créer. Pour créer un univers il faut de
l'harmonie, et il n'y a qu'un seul nombre capable de mettre de l'harmonie dans la différence, c'est le nombre d'Or. C'est pourquoi vous aurez besoin de sept sphères en Or pour représenter les nombres
dans tous leurs états.
Souvenez vous à la fin du Calcul d'Or Extra, à l'aide de la formule de Pythagore on a obtenu une fleur à
quatre pétales composée de spirales qui convergent toutes vers le centre du cercle que l'on nomme Taijitu symbole du Yin et Yang :
Pour mieux comprendre cette dualité que symbolise le Yin et Yang je vous propose d'observer le
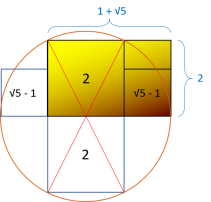
dallage ci-dessous qui met en évidence le lien physique qu'il y a entre des nombres irrationnels (√2) et des nombres entiers (2), et que l'on retrouve à
l'aide de la formule de Pythagore :
Autrement dit, que l'on travaille avec une seule dalle qui mesure 2 cm de longueur ou avec deux dalles
différentes qui mesurent chacune √2 cm de longueur, le résultat final est le même. En réalité ces deux dalles différentes (√2) sont complémentaires et leur assemblage donne naissance
à cette dalle unique (2) qui est l'union des deux et que l'on retrouve dans la démonstration géométrique de la formule de Pythagore.
Quand on regarde de plus près ces deux dalles complémentaires (noire et blanche), on se rend compte
rapidement qu'il y a une dualité géométrique qui les réunit et qui est la base même de leur complémentarité respective. En effet, il suffit de changer la forme d'une des deux dalles pour que la
deuxième prenne une forme différente que l'on peut appeler sa forme inverse, car en réalité toute forme possède une forme interne et une autre externe.
Nous vivons dans un monde rempli de matière. Là où certains voient du vide les scientifiques voient de
l'air, et c'est pour cette raison qu'il n'existe pas de verre à moitié plein ou à moitié vide, car l'autre moitié est forcément remplie d'air.
Quand on construit un objet, on a tendance à voir uniquement sa forme interne, or notre réalisation a des
conséquences sur la matière qui constitue l'objet et la matière qui l'entoure, d'où l'importance de la forme externe de tout objet.
On retrouve souvent cette dualité entre forme interne et forme externe dans les monuments anciens et
plus précisément au niveau de la partie supérieure de ces édifices, ce qui forme une dualité entre les pierres et l'air qui les entoure.
Du point de vue de la mesure des distances, les nombres ont tendance à suivre le même principe de dualité
en formant deux groupes distincts, séparant ainsi les nombres pairs des nombres impaires.
Mais il faut toujours garder à l'esprit que tout est pair, car en réalité les nombres impairs que nous
connaissons ne sont que le résultat d'une addition par adéquation des nombres pairs (voir Or Extra 1). Pour comprendre cela, il suffit de multiplier par 2 tous les nombres
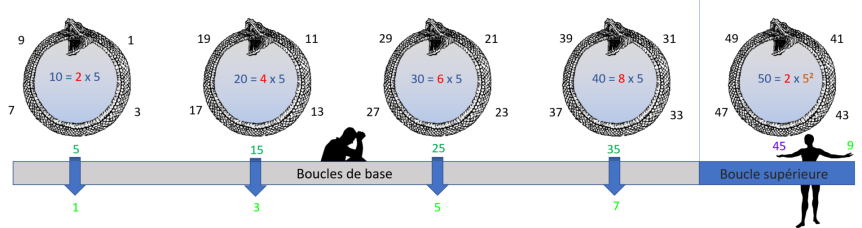
(1,2,3,4,5,6,7,8,9...) puis en soustraire 1 pour obtenir que des nombres impairs (1,3,5,7,9,11,13,15,17...) que l'on peut représenter sous forme de boucle indo-arabe réduite à 5 :
On remarque que la boucle ne peut être bouclée sans les nombres pairs, car en réalité les nombres impairs
tout comme les nombres pairs suivent la même opération d'addition qui correspond à +2, ce qui rend les nombres impairs des faux impairs ou plutôt des nombres résultants d'une addition par adéquation
aux nombres pairs. mais cela ne nous empêche pas de remarquer qu'à travers les multiples de 5 il y a une boucle de quatre chiffres impairs qui s'arrêtent au chiffre 7 pour ensuite faire apparaitre le
chiffre 9 dans la boucle supérieure.
Prenons maintenant la règle Or Extra 1 vue au chapitre 1 du livre "Or Extra" et essayons de faire
apparaitre les chiffres impairs.
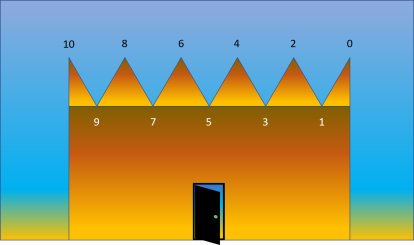
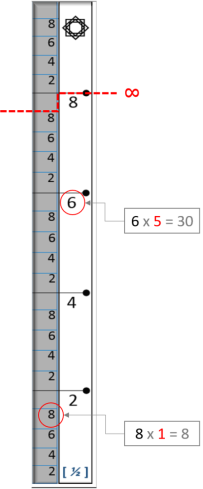
Le plus grand apport de cette règle est de pouvoir utiliser uniquement les quatre chiffres pairs (2,4,6 et
8) et non pas tous les nombres pairs (...,12,14,...,84,...), ce qui est devenu faisable grâce à cette boucle qui est bouclée à chaque fois qu'on arrive au chiffre 8. Cela signifie que dans un tel
système de mesure le plus grand nombre qui est l'infini est forcement le plus grand chiffre qui est le huit (8), raison pour laquelle de nos jours le symbole de l'infini est un huit couché
(ꝏ).
Cette règle utilise une unité de couple (1,5), mais pour la suite nous allons nous intéresser uniquement à l'unité de cinq, ainsi nous travaillerons avec une seule et unique unité
(5).
En gardant uniquement les graduations qui se situent à droite de la règle OR Extra 1 et qui représentent la
boucle supérieure qui a pour unité 5, on peut ajouter des graduations à gauche avec une nouvelle boucle qui représente les chiffres impairs et qui a la même unité 5.
En partant du principe que la boucle est bouclée au chiffre 8, et que l'infini ne peut être que le chiffre
8 dans un système utilisant uniquement les quatre chiffres pairs (2,4,6 et 8) on peut dire que le chiffre 9 est au-dessus de la boucle, ce qui signifie qu'il est plus grand que
l'infini.
Si les chiffres 8 et 9 sont les plus grands chiffres de la boucle, il convient donc de les utiliser
uniquement pour représenter l'infini et se contenter de travailler avec les chiffres allants de 1 à 7 pour les dimensions finies.
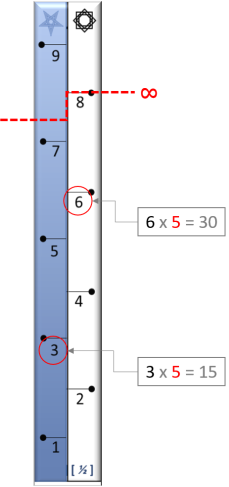
Il ne faut pas confondre la boucle des chiffres pairs (2468) avec la boucle des chiffres impairs (13579)
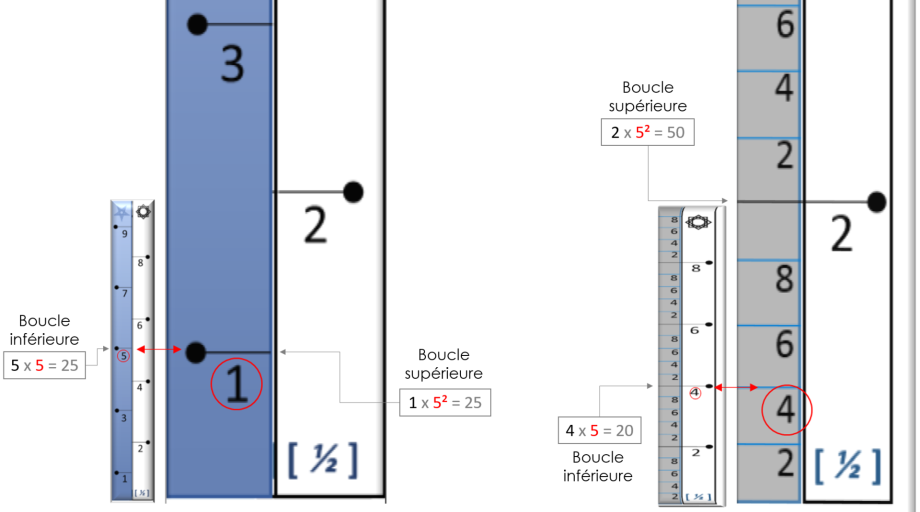
car elles sont complétement différentes et ne se comportent pas de la même façon. En effet, les chiffres pairs commencent par une boucle inférieure (unité 5) pour arriver à une boucle supérieure
(unité 52) qui vient s'ajouter par dessus, contrairement aux chiffres impairs qui commencent par une boucle inférieure (unité 5) pour arriver à une boucle supérieure (unité 52)
qui vient remplacer la boucle inférieure en transformant la graduation du 5 en 1.
Tout ce qui va de l'extérieur vers l'intérieur est InFernal, tout comme tout ce qui va de l'intérieur vers
l'extérieur est Or Extra. Cette transformation du 5 en 1 est InFernal car elle rend les chiffres impairs inaccessibles en cachant le chiffre 5 derrière l'unité 1, ce qui fait du chiffre 5 la porte
d'entré des chiffres impairs tout comme le chiffre 2 est la porte de sortie des chiffres pairs. Ce lien existant entre le chiffre 2 et le chiffre 5 est le résultat d'une multiplication par
adéquation, car multiplier par 5 ou diviser par 2 nous donne le même résultat à une virgule près :
De la même façon, on retrouve cette dualité entre le chiffre 2 et 5 en divisant l'unité
:
Cette relation entre les chiffres 1, 2 et 5
n'est que le résultat d'un système de numération à base de 10 que l'on nomme le système décimal, et c'est à cause de lui qu'on retrouve ces mêmes chiffres présents dans l'écriture du nombre d'or :
(1+√5) ÷ 2.
Alors dans ce deuxième livre nommé InFernal, vous allez devoir maîtriser l'usage des nombres d'or pour
pouvoir percer le mystère des chiffres impairs. Il va falloir donner un sens physique et mathématique à des géométries et des symboles que seul l'homme de l'antiquité en connaissait le
secret. Aucun texte sacré ne parle de ce qui va suivre, et pourtant vous allez êtres surpris de retrouver ce savoir orner les lieux de culte du monde entier.
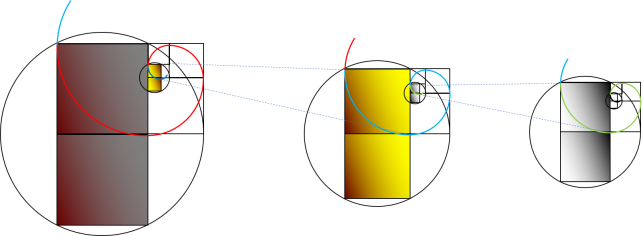
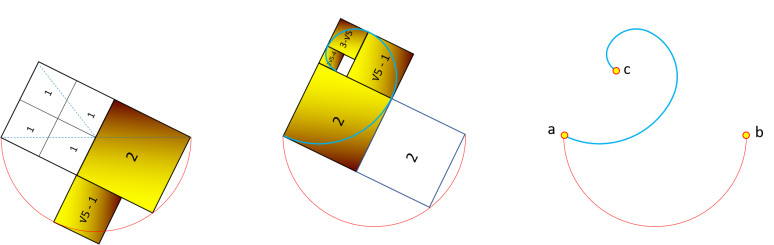
Intéressons nous maintenant au rectangle d'or et voyons de quels outils nous avons besoin pour étudier ce
type de géométrie. Sachant que le rectangle d'or est composé d'une infinité de carrés et que ces derniers forment une spirale sans fin, on peut dire qu'il suffit d'une équerre et d'un compas pour
mieux comprendre le lien qu'il y a entre les carré et les arcs de cercle qui constituent cette géométrie.
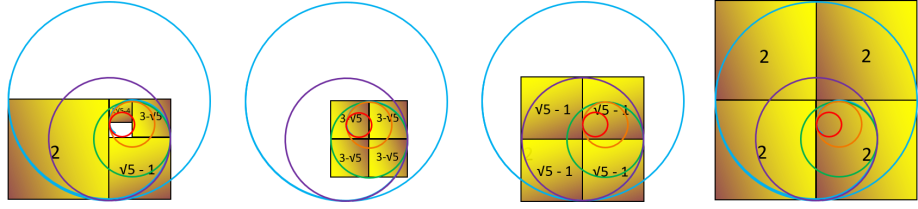
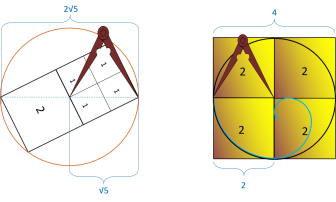
Commençons par la base du calcul d'Or Extra qui est le chiffre 2 et dessinons deux carrés identiques de
longueurs 2 constituants un bicarré. Ensuite il suffit de dessiner un cercle entourant ces deux carrés et ayant pour centre l'intersection des deux diagonales du bicarré pour obtenir un rectangle
d'or dans une des quatre directions possibles (en haut, en en bas, à droite et à gauche).
Ce cercle de construction qui nous permet de dessiner le rectangle d'or a pour diamètre la diagonale du
bicarré qui a une longueur de 2√5 (la diagonale d'un bicarré est égale à la longueur du carré multipliée par la racine de 5).
Nous avons donc ici un cercle qui a pour rayon la valeur de √5 qui est la diagonale d'un bicarré de 1. Encore une fois nous retrouvons cette relation entre ces trois chiffres 1, 2 et 5.
Ce qu'il faut retenir ici, c'est qu'à chaque fois que nous dessinons un cercle entourant un bicarré, ce
dernier a forcement pour diamètre la longueur du carré multipliée par √5, ce qui nous donne un lien directe entre les cercles de constructions et les carrés du
rectangle d'or qui est la racine de 5 :
Après avoir construit le rectangle d'or, nous pouvons faire apparaître la spirale du rectangle d'or en
dessinant les quarts de cercle qui se trouvent à l'intérieurs de chaque carré, et c'est exactement ce qui nous intéresse, car cette spirale est constituée d'arcs de cercle proportionnels aux carrés
appartenant au rectangle d'or.
A partir de quatre carrés consécutifs du rectangle d'or, on peut dire que la boucle est bouclée. En effet
ces quatre carrés forment un rectangle d'or mais pas seulement. En réalité nous sommes ici face à ce que nous allons nommer la deuxième loi de l'univers " tout est spirale
", et nous allons le prouver en utilisant la partie invisible des objets. Dans un premier temps nous allons prouver l'inverse, c'est à dire que nous partirons d'une spirale visible pour faire
apparaitre des carrés invisibles ainsi qu'un rectangle invisible.
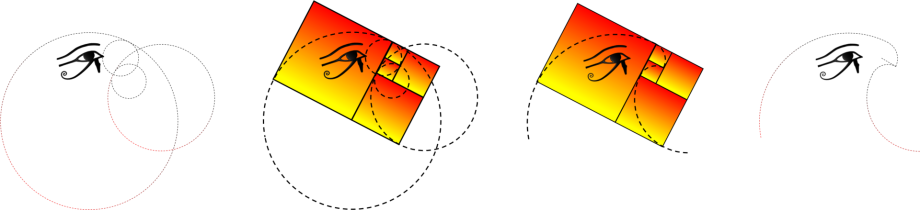
Prenons la spirale du rectangle d'or sans carrés ni rectangle. Il nous est difficile de lui trouver un lien
directe avec des carrés ou un rectangle quelconque, et pourtant celle ci est étroitement liée à ces deux géométries. Pour le voir il suffit de faire apparaitre les cercles tournants qui s'y
cachent.
Ce qui nous mène à la première loi de l'univers " l'éther est un ensemble de cercles tournants
les uns à l'intérieur des autres ", et qui nous permettra de trouver le lien invisible entre une spirale et sa géométrie.
Vous remarquerez que les cercles tournants associés à la spirale d'or forment toujours le symbole du
chiffre 6, une raison de plus pour dire que tout est six. Cependant à travers ces cercles nous pouvons faire apparaitre les carrés invisibles qui vont constituer notre rectangle
d'or.
Ce qu'il faut retenir ici, c'est que derrière chaque spirale se cache une géométrie, et derrière chaque
géométrie il y a des nombres, ce qui renforce l'idée que tout est nombre dans notre univers, exactement comme l'a prédit Pythagore il y a très longtemps.
Vous comprenez maintenant pourquoi nous parlons d'une partie visible et d'une autre invisible. Même
l'Égypte antique utilisait ces cercles invisibles pour faire ses plus belles sculptures, ce qui rendait la tâche très facile en se servant de l'éther.
Nous verrons dans le "Manuel d'Eau et de Ciel" pourquoi les anciennes civilisations s'intéressaient aux étoiles et le rapport qu'ils ont avec l'éther, ce qui déplaira certainement à
Albers Einstein, la personne qui a mit fin à ce concept. Mais en corrigeant sa célèbre formule à travers le livre "un Monde dans un Monde" il ne pourra qu'adhérer à ce principe
antique.
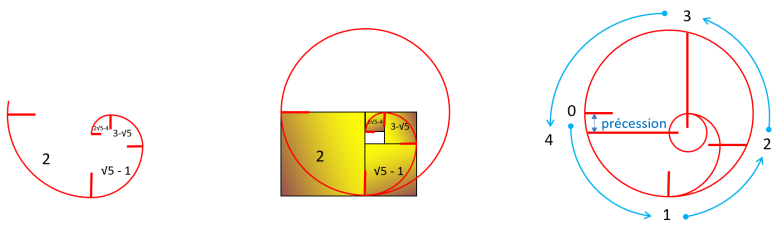
Revenons maintenant à la spirale du rectangle d'or et parlons de sa boucle d'or. Contrairement à ce que
nous enseigne l'école moderne qui considère qu'une période est forcément la durée nécessaire pour qu'un objet fasse un tour complet et revenir à son point de départ, la spirale d'or nous enseigne
qu'une période est la durée nécessaire pour qu'un objet fasse un tour complet correspondant à 2π sans
qu'il se retrouve forcément au même endroit qu'au départ. Ce phénomène nous l'appellerons la précession d'une spirale.
Cette précession à toujours lieu quand la boucle est bouclée, tout comme la précession des équinoxes à lieu
quand les quatre saisons de la Terre sont bouclées. Mais intéressons nous plutôt à cette boucle en terme de spirale et essayons de mesurer sa longueur. Pour cela nous allons avoir besoin des cercles
de construction qui vont nous permettre d'encadrer la boucle de manière efficace.
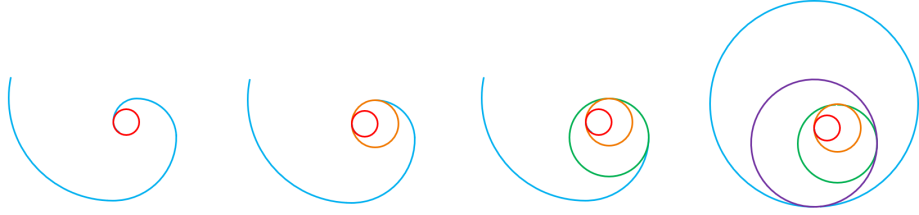
Règle d'Or N° 1 : toutes les spirales d'or ont une boucle et cette dernière est toujours bouclée quand un
de ses cercles de construction se retrouve à l'intérieur d'un autre cercle de construction. En partant du premier cercle qui est le plus grand des cercles de constructions, il nous faudra quatre
cercles consécutifs pour arriver au cinquième cercle qui est le plus petit et qui se trouve à l'intérieur du premier cercle.
Nous sommes ici face à la période d'une spirale d'or qui se répète sans fin à chaque
précession.
Nous arrivons maintenant à la partie la plus importante de cette boucle qui donne lieu à une précession.
Car souvenez vous, un cercle de construction à pour diamètre la diagonale d'un bicarré qui est 2√5, tandis que les arcs de la spirale d'or ont pour diamètre le double de la longueur du carré qui est 4.
Nous utiliserons par la suite uniquement les rayons des cercles de construction et des arcs de la spirale
d'Or, ce qui nous permettra de calculer plus facilement les circonférences des cercles et des arcs en question pour trouver une relation entre la longueur de la spirale d'or et son premier cercle de
construction.
Nous verrons par la suite que cette relation est le résultat d'une harmonie établie par les nombres
d'or.
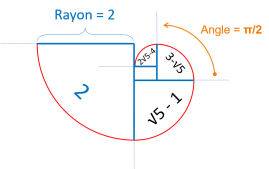
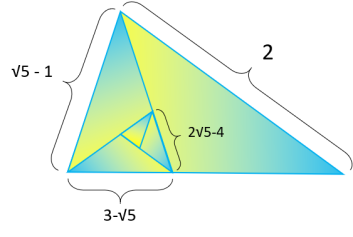
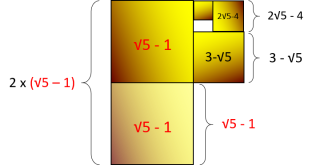
Pour mesurer la longueur de cette spirale d'or, nous commençons par mesurer la longueur de chacun des
quatre arcs qui la constituent. Pour cela il suffit de multiplier le rayon de chaque arc par son angle qui est toujours égale à π/2 dans le cas de la spiarle du rectangle d'or.
La longueur de la spirale d'or Ls est égale à la somme des longueurs d'arcs
Li :
-
Premier arc : L1 = 2π/2
-
Deuxième arc : L2 = (√5 - 1)π/2
-
Troisième arc : L3 = (3 - √5)π/2
-
Quatrième arc : L4 = (2√5 - 4)π/2
Ls = L1+L2+L3+L4
= (2 + (√5 - 1) + (3 - √5) + (2√5 - 4))π/2
= (2 - 1 + 3 - 4 + √5 - √5 +2√5)π/2
= (2√5)π/2
Ls = (√5)π
Cette longueur Ls vous fait penser certainement au premier cercle de construction qui a
un rayon égale à √5. Essayons de mesurer la longueur (circonférence) de son demi-cercle qui a un angle
de π :
-
Ldemi-cercle = rayon x angle = (√5)π
On peut donc dire que la longueur de la spirale d'or est égale à la longueur du premier demi-cercle de
construction, Ls = Ldemi-cercle avec Ls la distance allant du point a au point c et
Ldemi-cercle la distance allant du point a au point b.
Cette relation entre le premier demi-cercle de construction et la période de la spirale d'or est due aux
nombres d'or, car en additionnant quatre nombres d'or consécutifs (allant du plus grand au plus petit) nous obtenons toujours un résultat correspondant au premier nombre d'or multiplié par
√5 :
Somme1 = 2 +
(√5 -
1) + (3 - √5) + (2√5 - 4)
= 2 - 1 + 3 - 4 + √5 - √5 +2√5
= 2 x √5
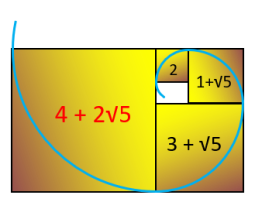
Prenons maintenant les quatre nombres d'or allants de (4 + 2√5) à 2 :
Somme2 = (4 + 2√5) + (3 + √5) + (1
+ √5)
+ 2
= 4 + 3 + 1 + 2 + 2√5 + √5 + √5
= 10 + 4 √5
= (4 + 2√5) x √5
Souvenez vous, a la fin du chapitre 3 du calcul d'or extra nous avons trouvé la même relation à l'aide du
Birectangle d'Or Extra :
(4 + 2√5) x √5 = (4 + 2√5) + (3 + √5) + (1 + √5) + 2
= (4 + 2√5) + (3 + √5) + (3 + √5)
= (4 + 2√5) + 2 x (3 + √5)
Vous avez certainement remarqué que depuis le début nous utilisons toujours une période qui commence par
des chiffres pairs (4+2√5) et se termine par d'autres chiffres pairs (2). Ce choix n'est pas le fruit du hasard, car il est évident d'utiliser uniquement des chiffres pairs dans
un calcul d'Or Extra.
En effet, la couverture du livre " Calcul d'Or Extra " nous montre une spirale avec des
chiffres paire (2486) sans jamais en parler tout au long du livre. Cette spirale est la première clef nécessaire pour avoir accès à un endroit scientifiquement improbable, c'est ce qui
fait d'elle une énigme très difficile.
Tout vient à point à qui sait attendre. Maintenant que nous connaissons la période de la spirale d'or, nous
allons pouvoir en apprendre un peu plus sur cette spirale du calcul d'Or Extra. Il existe quatre possibilités de choix pour la période d'une spirale d'or, en fonction de l'orientation que nous
souhaitons donner à notre spirale :
Comme il nous est interdit d'utiliser les nombres impairs dans un calcul d'Or Extra, nous allons dans un
premier temps choisir uniquement les quatre possibilités qui forment la boucle 2486 et qui donnent lieu à quatre périodes commençant par des chiffres pairs et se terminant par d'autres chiffres pairs
:
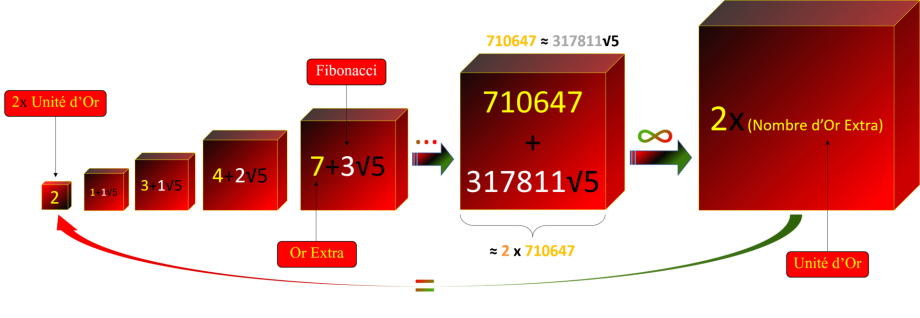
Tous les nombres d'or sont pairs car ils sont les doubles des nombres d'Or Extra, c'est ce que nous avons
démontré au chapitre 3 du livre " Calcul d'Or Extra ".
nous savons très bien que les nombres d'or commencent par le chiffre 2, mais l'erreur que nous faisons tous c'est
de penser que l'unité est égale à 1, ce qui est faux car la spirale d'or passe forcément par une série de nombres avant d'arriver au chiffre 2. En effet avant d'arriver au 2, nous avons plusieurs
additions entre les nombres d'Or Extra et les nombres de Fibonacci multipliés par racine de cinq, ces deux derniers se rapprochent de plus en plus au fur et à mesure qu'on avance dans la spirale d'or
jusqu'à qu'ils deviennent égales, autrement dit jusqu'au moment où l'addition des deux devient égale à deux fois les nombres d'Or Extra, car tout simplement les nombres de Fibonacci multipliés par
racine de cinq deviennent des nombres entiers égales aux nombre d'Or Extra. A ce moment précis nous atteignons l'unité d'Or, qui d'un coté représente la valeur des nombres d'or à l'infini et de
l'autre coté représente l'unité par où tout a commencé.
L'infini n'existe pas, ou disons plutôt que la science moderne l'utilise pour se faciliter la tâche, ce
qui nous induit forcement à une erreur dimensionnelle dans un monde où tout a une dimension. D'où l'importance de cette constance dynamique qui est l'Unité d'Or, une constance capable de s'adapter à
toutes les situations.
L'Unité d'Or est la limite de l'infini, la limite que nous imposons à un calcul en fonction de la situation
où nous nous trouvons. Tout comme une calculatrice est limitée à un nombre de décimales, les astres sont limités à des distances que l'on peut assimiler à la limite de précision d'une calculatrice
scientifique. Prenons par exemple le nombre d'Or Extra 4870847, il est la limite de la plus part des calculatrices scientifiques que les matheux utilisent, car en considérant ce nombre comme Unité
d'Or tout les nombres d'or deviennent des nombres pairs, et pourtant cela reste scientifiquement impossible pour les nombres d'or qui sont des nombres irrationnels.
Ceci est très important à comprendre et à retenir, car quand nous travaillerons sur le soleil et les
étoiles, nous manipulerons les lois de la physique à l'aide de cette Unité d'Or et en fonction des saisons, mais nous ferons tout cela de préférence la nuit (voir "Manuel d'Eau et de
Ciel").
Pour la suite, nous allons travailler uniquement avec le double des nombres d'Or Extra tout en gardant à
l'esprit que l'unité est l'Unité d'Or qui est choisie en fonction de notre situation. Notre objectif ici est de simplifier les calculs tout en donnant une limite à l'infinie.
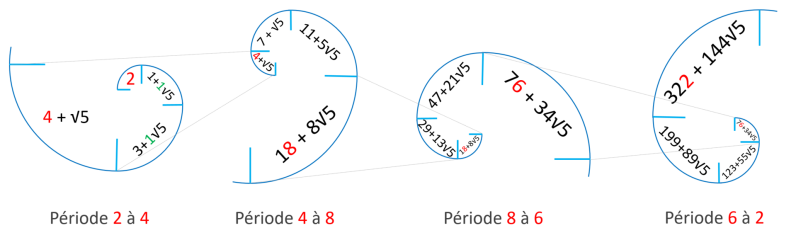
Revenons maintenant à la période de la spirale d'or et calculons les longueurs des quatre périodes
Lpi qui forment la boucle :
-
Lp1 = 2 + 6 + 8 + 14 = 30
= 6 x 5 = 3 x 10
-
Lp2 = 14 + 22 + 36 + 58 = 130 = 26 x
5 = 13 x 10
-
Lp3 = 58 + 94 + 152 + 246 = 550 = 110 x 5 =
55 x 10
-
Lp4 = 246 + 398 + 644 + 1042 = 2330 = 466 x 5
= 233 x 10
Vous avez certainement remarqué que toutes les longueurs des périodes Lpi sont des
multiples du chiffre cinq, mais le plus important
est de noter que toutes les périodes sont des nombres de Fibonacci multipliés par 10. La présence des nombres de Fibonacci est le résultat du Birectangle d'Or Extra :
Lp1 = 2 x ( (1 + 3) + 4 +
7 ) = 2 x ( 4 + 4 + 7 ) = 2 x 15 = 2 x 3 x 5 = 2 x ( 3 √5 ) x √5.
Rassurez vous, vous aurez le temps de maitriser toutes ces notions des nombres d'or à travers nos livres.
Allons maintenant découvrir un autre univers, autre que le calcul d'Or Extra, le monde InFernal des nombres.
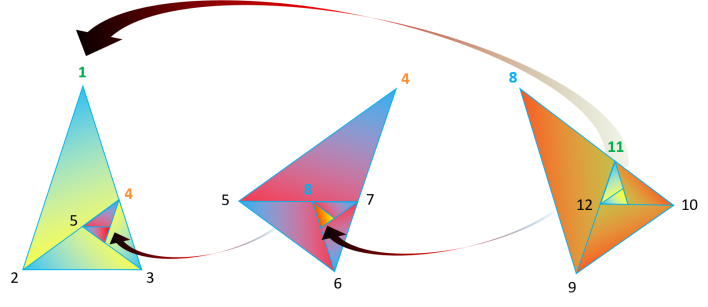
Pour la première fois nous allons étudier une géométrie que vous connaissez tous sous le nom du triangle
d'or et qui sera notre première géométrie InFernal. Nous prossèderons de la même façon que pour le rectangle d'or en passant par les cercles de construction pour arriver à la période de cette spirale
InFernal du rectangle d'or.
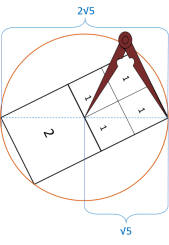
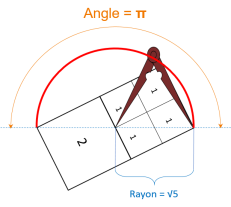
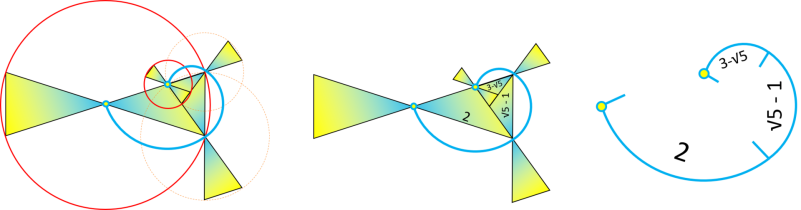
Pour commencer nous dessinons le premier cercle de construction de rayon 2, ensuite en prenant comme
centre le milieu de son rayon nous traçons un nouveau cercle de rayon √5, ce qui nous permet d'obtenir un carré de longueur √5-1, ensuite il suffit de tracer un cercle de rayon √5-1 avec son
centre situé sur notre premier cercle de construction pour obtenir trois points formant un triangle d'or.
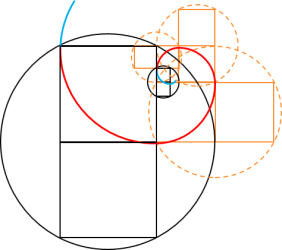
Tout comme pour le rectangle d'or, un cercle de construction du triangle d'or entoure toujours deux
triangles d'or. Pour obtenir tous les cercles de construction en partant du premier, il suffit de tracer un cercle qui a pour rayon la base du premier triangle et pour centre une des deux extrémité
de sa base.
Nous remarquons que pour le triangle d'or le quatrième cercle de construction se retrouve à l'intérieur du
premier, contrairement au rectangle d'or où c'est le cinquième cercle de construction qui se retrouve à l'intérieur du premier. Mais le principe des cercles tournants reste le même pour ces deux
géométries d'or, avec tout de même une différence au niveau des arcs de cercle qui possèdent des angles plus petits.
Nous verrons par la suite qu'il ne suffit pas qu'un cercle de construction se retrouve à l'intérieur d'un
autre pour trouver la période d'une spirale, mais cette boucle reste comme même très importante pour comprendre le lien existant entre le triangle d'or et le rectangle d'or .
Cette boucle est constituée des trois premiers nombres d'or :
-
Somme1 = 2 + (√5 - 1) + (3 - √5)
= 2 - 1 + 3
+ √5
- √5
= 4
=
2 x 2
En réalité vous prenez n'importe quel nombre d'or, la somme de trois nombres consécutifs est égale au
double du plus grand terme :
Somme2 = (√5 - 1) + (3 - √5) +
(2√5 - 4)
= - 1 + 3 - 4 + √5 - √5 +2√5
= 2√5 - 2
= (√5 - 1) x 2
Il est temps maintenant de mesurer la longueur de cette boucle en spirale du rectangle d'or et qui est
constituée de trois arcs de cercle.
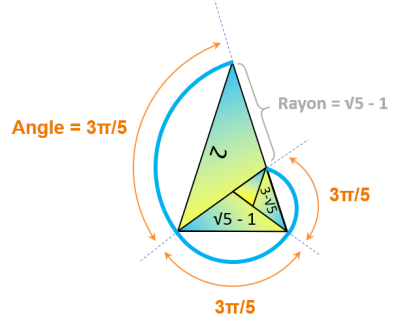
Un triangle d'or est constitué d'une infinité de triangles d'argent qui ont chacun une base égale à un
nombre d'or et un angle égale à 3π/5 correspondant à un arcs de spirale.
Pour chaque triangle d'argent, Le rayon de son arc de cercle correspond au nombre d'or précèdent sa base
:
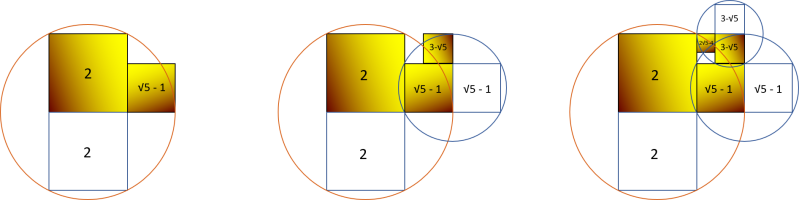
-
Premier arc de base 2 : L1 = (√5 - 1) x 3π/5
-
Deuxième arc de base (√5 - 1) : L2 = (3 - √5) x 3π/5
-
Troisième arc de base (3 - √5)
: L3 = (2√5 -
4) x 3π/5
Ls = L1 + L2 + L3 = ( (√5 - 1) + (3 - √5) + (2√5 - 4) ) x 3π/5
= 2 x (√5 - 1) x 3π/5
Ls= (√5 - 1) x 6π/5
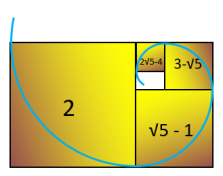
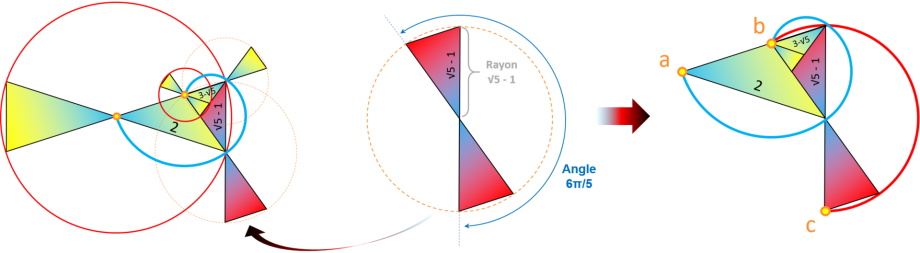
Maintenant nous allons chercher la relation entre cette longueur de spirale Ls et nos
trois cercles de construction. Pour cela nous allons juste identifier l'unique cercle de construction possédant le nombre d'or (√5 - 1) et voir à quoi correspond
l'angle 6π/5.
C'est effectivement le deuxième cercle de construction qui possède un rayon
de (√5 - 1) et avec un angle de 6π/5 on retrouve la longueur
de notre spirale Ls. L'arc du deuxième cercle de construction renfermant les deux triangles d'or symétriques et allant du point c à au point b, a la même longueur que la spirale du triangle d'or allant du point a au point b.
Il faut noter que le deuxième cercle de construction a le même rayon que le premier cercle tournant qui
forme cette spirale InFernal, car en effet nous retrouvons tous les cercles tournants dans les cercles de construction.
Ce qui nous rappelle que la longueur de la spirale Ls est égale au double de la longueur
d'arc du premier cercle tournant :
-
Ls= (√5 - 1) x 6π/5 = 2 x (√5 - 1) 3π/5 = 2 x
L1
Cette boucle formée par trois arcs de cercle n'est pas une période, mais elle a toute son importance pour
les chapitres à venir. Allons voir maintenant la vraie période de cette spirale du triangle d'or.
Il nous faudra dix triangles d'or pour arriver au onzième triangle possédant la même orientation que le
premier triangle du départ. Cette configuration est très intéressante car elle reflète le système indo-arabe qui est la base décimale.
Nous allons maintenant mesurer la longueur de cette période qui est la somme des arcs correspondant au dix
premiers nombres d'or :
Lp = Somme de dix nombres d'or
= ((√5-1)+(3-√5)+(2√5-4)+(7-3√5)+(5√5-11)+(18-8√5)+(13√5-29)+(47-21√5)+(34√5-76)+(123-55√5)) x 3π/5
= (77 -
33√5) x 3π/5
= 11 x (7 - 3√5) x 3π/5
Cela signifie qu'il de prendre la longueur du quatrième arc de spirale et de la multiplier par 11 pour
obtenir la longueur totale de la période de la spirale du rectangle d'or.
C'est ce qui rendre ce quatrième cercle de construction intéressant, car il contient tout ce dont nous avons
besoin pour connaître le comportement de cette géométrie InFernal.
Dans ce chapitre, notre objectif est de bien maîtriser les bases des nombres d'or tout en ayant une vision
géométrique sur ces deux spirales de comportements différents, une spirale basée sur le rectangle d'or et une autre basée sur le triangle d'or, mais qui en réalité restent liées à jamais par une
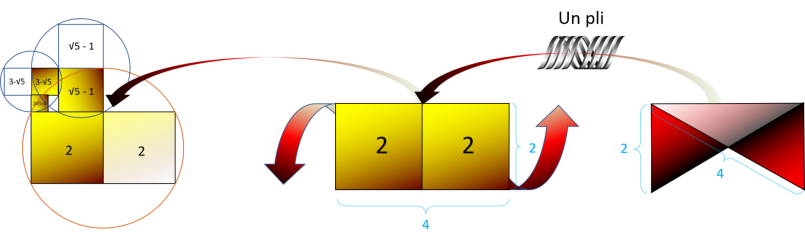
géométrie que nous allons nommer le triangle InFernal.
La lumière n'existe pas, la couleur non plus, et cette notion ne date pas d'aujourd'hui, les anciens le savaient et
les plus intelligents parmi eux sont allés encore plus loin en faisant de l'obscurité une nouvelle lumière qui restera à jamais invisible pour l'humain que nous sommes.
Au chapitre suivant nous allons apprendre à maîtriser cette géométrie du triangle InFernal qui est la base même de
ce que nous appelons un objet et qui n'est ni plus ni moins qu'un reflet renfermé sur lui même grâce à un nœud. Mais on ne peut parler de nœud sans parler de pli, et c'est à ce moment là où la géométrie du rectangle d'or prend toute son
importance.
Vous êtes sur le point de comprendre pourquoi tous ceux qui prétendent avoir un savoir secret utilisent
des nœuds dans leurs plus belles figures. Les Mayas, les pharaons, les sumériens voir même les
frants-maçons utilisent tous le même langage pour faire illusion à un savoir perdu que personne de nos jours ne peut déchiffrer mais le chapitre 3 de ce livre vous en apprendra un peu plus sur cette
géométrie des nœuds.