Les nombres d'or
En cherchant bien, Vous trouverez en toute chose un couple en or.
Divine proportion, section dorée ou nombre d'or, ce sont des termes qui désignent un rapport arithmétique que l'on note généralement φ (phi) en hommage au sculpteur grec Phidias qui décora le Parthénon à Athènes avec notamment la statue d'Athéna qui montre la présence du nombre d'or. Mais ce nombre est connu depuis la nuit des temps, bien avant la construction de la pyramide de Khéops avec ses dimensions très attachées à la section dorée on retrouve le temple d'Andros sous la mer des Bahamas qui serait la première manifestation de ce nombre divin il y a 10 000 ans.
Comme le titre l'indique, nous parlerons ici des nombres d'or et non pas uniquement d'un seul et unique nombre. Car en réalité le nombre d'or que vous connaissez est un rapport qui n'est ni une dimension ni une mesure, ce qui est un problème en soi pour un architecte qui a besoin d'utiliser des instruments de mesure pour respecter certaines dimensions, et pour cause, les bâtisseurs de cathédrales du moyen-âge n'ont jamais utilisé le système métrique ou son équivalant pour réaliser leurs œuvres car il préféraient utiliser les dimensions du corps humain (la paume, la palme, l'empan, le pied et la coudée) ou un autre système de mesure issu du nombre d'or (suite des pentagones présents dans le triangle d'or).
Toute architecture est le résultat d'un assemblage entres plusieurs dimensions. Utiliser un rapport entre ses dimensions permet d'introduire une harmonie dans l'ensemble.
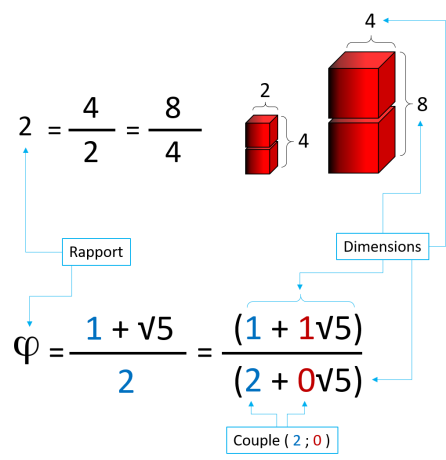
Un rapport est la division d'une dimension par une autre, ainsi pour un même rapport on a une infinité de dimensions (rapport de 2 pour 4 sur 2 ou 8 sur 4).
Le nombre d'or n'est donc que le rapport entre deux dimensions que l'on va nommer les dimensions d'or. Ces dernières sont constituées d'un couple de nombres qui sont les nombres d'or.
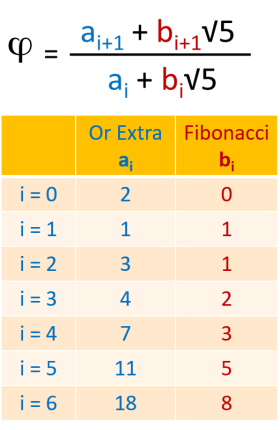
Pour l'instant intéressons nous uniquement aux nombres entiers et ignorons la racine de cinq. Les nombres d'or sont donc une série de couples constitués de nombres entiers, ou un couple de deux séries de nombres entiers (série de Fibonacci et série d'Or Extra) :
On peut donc définir une écriture générale du nombre d'or à l'aide des deux suites ai (suite d'Or Extra) et bi (suite de Fibonacci), et chercher le lien caché entre ces deux suites.
En regardant de plus près les termes de ces deux suites, on s'aperçoit très rapidement qu'il y a plusieurs liens entres ces nombres :
-
11 + 5 = 2 x 8, ou de manière générale ai + bi = 2 x bi+1.
-
11 + 5 x 5 = 2 x 18, ou de manière générale ai + 5 x bi = 2 x ai+1.
Pour la suite de ce cours nous allons nous intéresser uniquement à la première relation ( ai + bi = 2 x bi+1), ce qui est largement suffisant pour découvrir de nouvelles séries de nombres d'or.
Tout ce que nous venons de voir ici n'est qu'un rappel de ce qui est dit dans le livre "Or Extra". Passons maintenant à la pratique et essayons de découvrir de nouveaux nombres d'or autres que ceux de Fibonacci ou d'Or Extra.
Pour y parvenir nous allons utiliser la relation (ai + bi = 2 x bi+1) pour trouver des nombres liés par cette même relation. Ce qui signifie qu'il suffit de partir d'un nombre pair (2xbi+1) et le décomposer en somme de deux entiers (ai+bi) pour trouver une série de couples de nombres d'or (ai , bi).
Prenons par exemple le nombre 6 qui est un nombre pair, et décomposons le en somme de deux nombres entiers (1 + 5 = 6):
-
1 + 5 = 2 x 3, ce qui vérifie la relation ai + bi = 2 x bi+1.
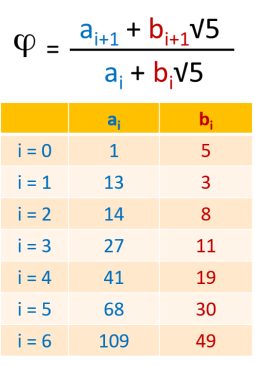
Cela nous donne le premier terme de la suite ai qui est le 1, et les deux premiers termes de la suite bi qui sont le 5 et le 3.
Pour trouver les termes restants de la suite bi il suffit d'additionner les deux premiers termes (5+3) pour obtenir le troisième terme (8) et ainsi de suite jusqu'à obtenir tous les termes de la suite bi (3+8=11;8+11=19;...).
concernant les termes de la suite ai il suffit de transformer la relation ai+bi =2xbi+1 en ai=2xbi+1-bi ce qui donne a1=13 avec 13=16 - 3= 2 x 8 - 3. En suite, en sommant les deux premiers termes (1 et 13) on obtient le troisième terme (14), et ainsi de suite jusqu'à obtenir tous les termes de la suite ai.
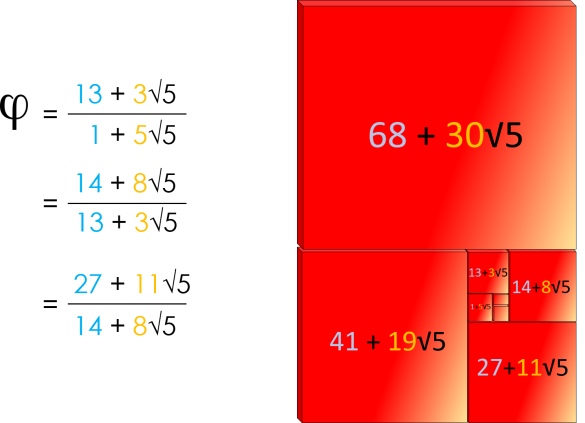
Désormais nous pouvons dessiner notre rectangle d'or à l'aide des nombres d'or obtenus ci-dessus :
Cette méthode basée sur le relation (ai + bi = 2 x bi+1) permet d'obtenir une infinité de nombres d'or qui respectent en même temps la relation (ai + 5 x bi = 2 x ai+1). Pour les trouver, Il suffit de partir d'un nombre pair et le décomposer en somme de deux nombres entiers.
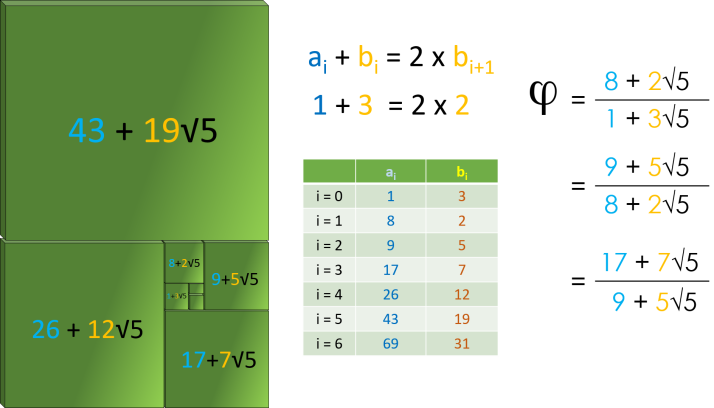
Prenons maintenant un autre exemple en partant de l'égalité 1+3=2x2 :