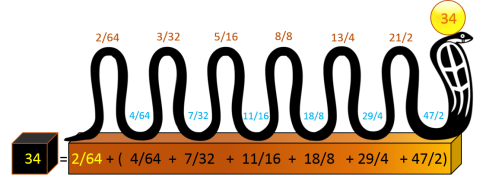Or Extra 2
Maintenant que vous savez comment passer d'une mesure scientifique à une mesure par Calcul d'Or
Extra, vous allez faire un voyage dans le passé, en explorant le savoir d'une grande civilisation antique, et percer
le mystère de l'œil d'Horus (œil oudjat).
En réalité vous allez juste mettre en pratique le Calcul d'Or
Extra sur cette suite mathématique pour enfin trouver ce nombre d'Or si présent dans les plus vieux monuments historiques de notre monde.
Vous avez certainement remarqué dans le chapitre
précèdent qu'une mesure scientifique utilise des graduations qui correspondent à l'opération +1, alors que le Calcul d'Or Extra utilisait l'opération +2.
C'est dans cette Deuxième partie que vous allez vous rendre compte de l'utilité des nombres
pairs. Il sont indispensables pour le passage d'une mesure basée sur une opération d'addition (+), à une autre de multiplication (x).
Pour toute mesure de distance, il convient d'utiliser une unité égale à 1, ce qui permet d'accéder à
tous les nombres par l'opération d'addition ( 1+1=2, 2+1=3, 3+1=4,... etc).
Or pour une mesure de surface, l'unité égale à 1 cache les autres
nombres pendant l'opération de multiplication (1 x 1 = 1), car une surface utilise le carré de l'unité.
Avec la base du Calcul d'Or Extra, le chiffre 2, on obtient tous les nombres résultants de cette opération
de multiplication (2x2=4, 4x2=8, 8x2=16,...etc) qui sont représentés à travers le Carré d'Horus ci-dessous.
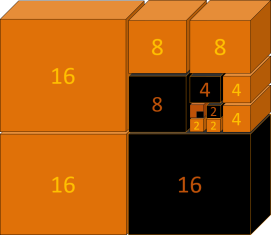 Carré d'Horus
Carré d'Horus
Cette représentation sous forme de carré nous montre l'existence de deux séries de nombres (orange/Noir),
elle sont liées par une relation de tiers (l'une est le double de l'autre).
En réalité il y a deux spirales complémentaires :
-
Les multiples de 2.
-
Les multiples de 6.
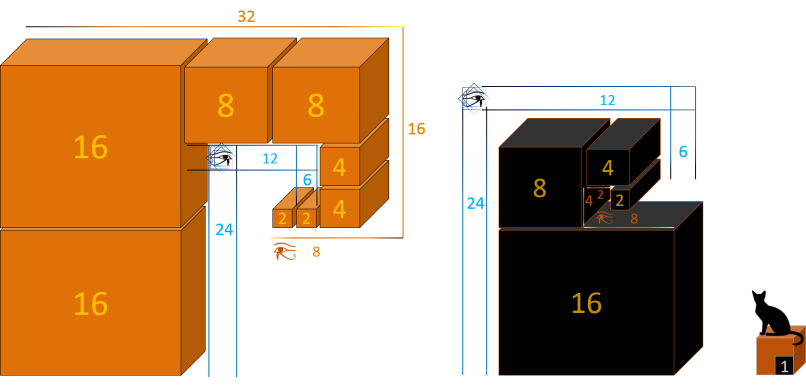 Décomposition en Rectangle d'Horus
Décomposition en Rectangle d'Horus
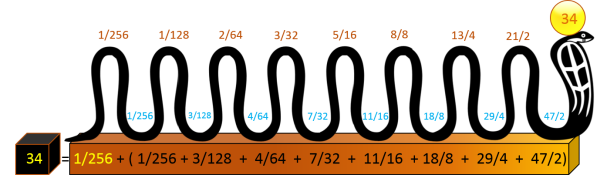
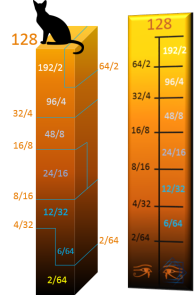 Règle d'Horus
Règle d'Horus
La décomposition en Rectangle d'Horus ci-dessus, permet d'identifier ces deux spirales :
-
Spirale externe, qui correspond aux multiples de 2 (nombres en orange).
-
Spirale interne, qui correspond aux multiples de 6 (nombres en bleu).
Elle sont liées à jamais par la suite d'Horus (1/2)+(1/4)+(1/8)+(1/16)+(1/32)+(1/64).
Cette suite correspond au lien existant entre les graduations et les
écarts entre ces mêmes graduations:
-
Graduation : correspond à la hauteur, elle est toujours un multiples de 2
(au numérateur).
-
Ecart : correspond à la distance entre deux graduations consécutives, il est toujours un multiples de 6
(au numérateur).
-
Ecarts et graduations sont toujours des multiples de 2 (dénominateur).
Chaque graduation est égale à la précédente additionnée à l'écart qu'il y a entre les deux
:
-
2/64 + 6/64 = 8/64 = 4/32
-
4/32 + 12/32 = 16/32 = 8/16
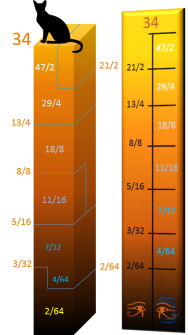 Règle d'Or Extra 2
Règle d'Or Extra 2
En intégrant la suite de Fibonacci dans celle d'Horus, on obtient la règle d'Or Extra 2, avec les
nombres de Fibonacci (...,2,3,5,8,13,...) représentants les graduations (hauteurs), et les nombres d'Or Extra (...,4,7,11,18,29,...) représentants les écarts :
-
2/64 + 4/64 = 6/64 = 3/32
-
3/32 + 7/32 = 10/32 = 5/16
-
5/16 + 11/16 = 16/16 = 8/8
-
8/8 + 18/8 = 26/8 = 13/4
-
13/4 + 29/4 = 42/4 = 21/2
-
21/2 + 47/2 = 68/2 = 34
Le dénominateur des
graduations et des écarts, est le même que sur la règle d'Horus (multiple de 2).
La règle d'Or Extra 2, permet la décomposition en éléments simples des nombres de
Fibonacci.
Cet arrangement numérique entre hauteurs et écarts n'a pas de limite.
Pour une seule et même
hauteur donnée (34), il existe plusieurs décompositions possibles.
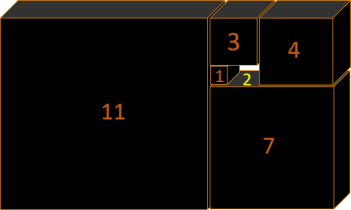 Rectangle d'Or Extra
Rectangle d'Or Extra
Le Rectangle ci-contre, est la représentation
géométrique des nombres d'Or Extra. il représente la suite manquante à la suite de Fibonacci pour compléter
le nombre d'or, qui a besoin de ces deux suites complémentaires pour exister tout comme le Carré d'Horus avec ses
deux spirales interne et externe.
 Règle d'Or Extra 2
Règle d'Or Extra 2
Les nombres d'Or Extra tout comme les nombres de Fibonacci tendent vers le nombre d'or, ensuite à partir de
ce nombre ((1+√5)/2), les nombres se répètent en faisant apparaitre les deux suites avec une relation de couple :
-
Suite d'Or Extra = SE
-
Suite de Fibonacci = SF
-
Couple (homme, Femme) = (SE ,SF)
-
Unité du couple = UC = (UE , UF) = (1
, √5)
-
Union du couple : ( UE² + UF² ) = 6
Les deux suites Or Extra et Fibonacci, ont chacune sa propre unité surfacique mais leur somme est
toujours un multiple de 6. L'unité peut être
n'importe quelle surface, elle varie en fonction de l'unité du couple choisie, tout en restant un multiple de √5 :
-
UF = √5 x UE ( si UE = √5
donc UF = 5 )
Tous les couples sont représentés sur la règle d'Or Extra ci-contre, avec à chaque niveau un couple d'Or
(E,F), ainsi le rapport (division) entre deux couples consécutifs est égale au nombre d'Or :
-
Couple niveau 4 : (7,3)
-
Couple niveau 3 : (4,2)
-
UC = (1 , √5)
-
Rapport (division) : (7+3√5) / (4+2√5) = 1,61803398875.........
Le rectangle d'Or Parfait ci-dessous, illustre bien cette liaison entre la suite de Fibonacci et la suite
d'Or Extra.
 Rectangle d'Or Parfait
Rectangle d'Or Parfait
Ce rectangle d'Or Parfait, est le sujet du chapitre suivant. On remarque la présence du chiffre 5 dans les
deux premières parties du Calcul d'Or Extra, il concerne l'unité du couple, il est toujours caché sous le chiffre 6 qui est l'union du couple :
-
En distance (première partie) sous la forme : 1 + 5 = 6
-
En surface (deuxième partie) sous la forme : 1² + (√5 )² =
6
Ce chiffre mystérieux qui est le 5, est présent partout sans jamais être accessible. Il est le discriminant
qui offre cette solution positive appelée nombre d'or :