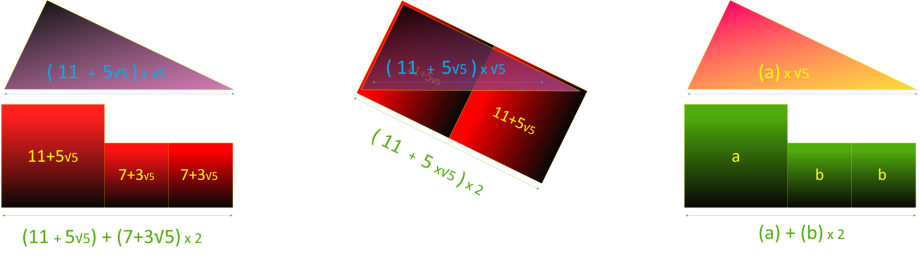Or Extra 3
Un calcul scientifique utilise le chiffre
Zéro pour débuter chaque période (0,10,20,30,...).
Or pour le Calcul d'Or Extra
:
-
Le chiffre Zéro n'existe pas.
-
Le chiffre 2 est la base pour toute
mesure.
-
Le chiffre 6 est l'union du couple.
En réalité tout est 6 dans l'univers, ce chiffre est plus qu'un
nombre, il représente toutes les spirales possibles d'un point de vue mathématique. Quand vous observez le soleil, vous surfez à l'intérieur de cette
spirale selon la loi en Carré Inverse d'Isaac Newton.
Avant de s'attaquer à cette loi en Carrée Inverse, dans cette
Troisième Partie du Calcul d'Or Extra, vous allez devoir plonger dans la spirale du Rectangle d'Or, et voir encore plus loin que Fibonacci, pour enfin
remarquer ce que certainement Al-Khâwarizmî avait remarqué durant ses recherches pour donner naissance à l'Algèbre.
Le
nombre d'or est une proportion, qui correspond au nombre réel positif que l'on note généralement φ. Ce nombre est irrationnel, il ne peut donc pas s'écrire sous la forme d'une
fraction  avec a et b deux nombres
entiers.
avec a et b deux nombres
entiers.
Il est aussi l'unique solution positive à l'équation du second degré x2 - x - 1 =
0.
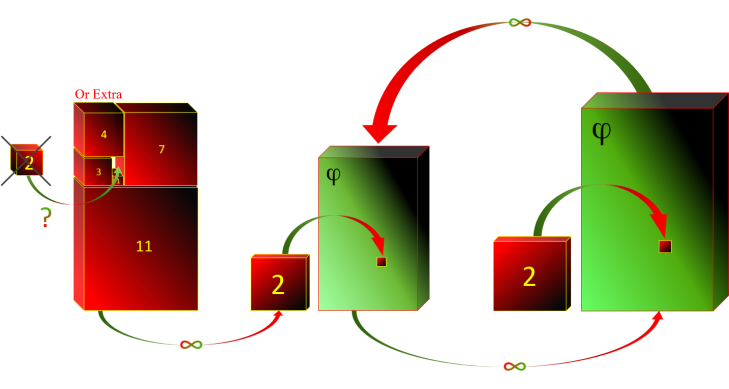
La suite de Fibonacci est une suite d'entiers qui tend vers ce nombre d'or. Chacun de ses termes correspond
à la somme des deux termes précédents, comme le montre le rectangle de Fibonacci ci-dessous.
 Rectangle de Fibonacci
Rectangle de Fibonacci
Le rectangle de Fibonacci est composé uniquement de carrés qui commencent par 1 et 1, suivi de 2 pour
tendre vers le Rectangle d'or Parfait :
 Rectangle d'Or Parfait
Rectangle d'Or Parfait
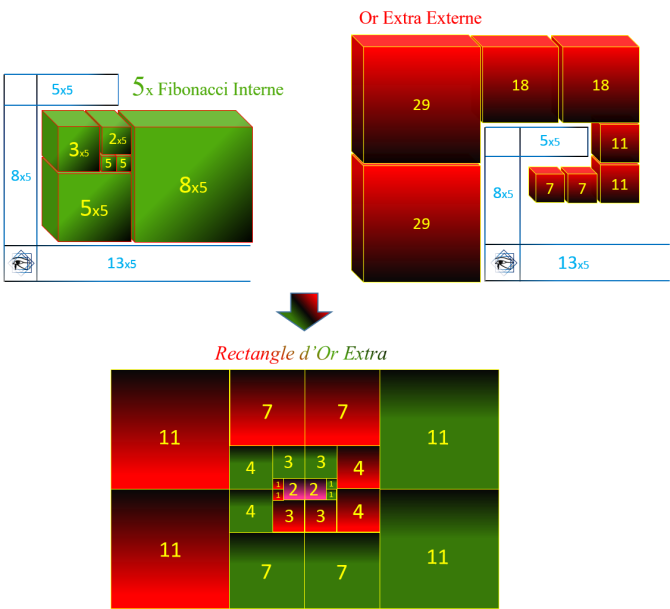
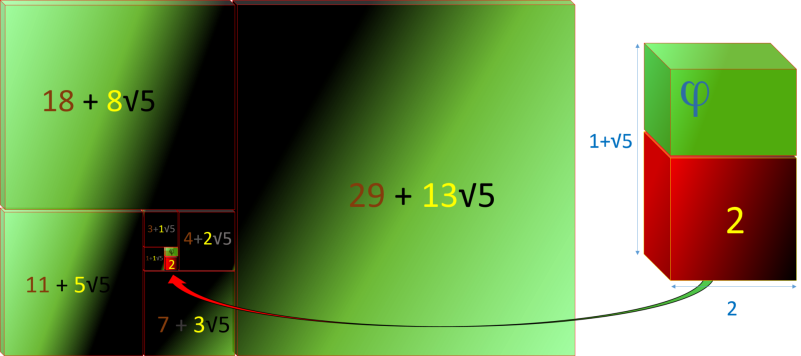
Le Rectangle d'Or Parfait, commence par l'unique carré entier le 2, suivi par une suite de nombres
irrationnels, somme des termes de la suite Or Extra et la suite de Fibonacci multipliée par √5.
Rappelons que le nombre d'Or, est l'unique solution positive à l'équation
:
Or le Rectangle d'Or Parfait, nous donne une infinité de rectangles de tailles différentes, et qui sont
tous aux proportions du nombre d'or. Donc ces rectangles représentent tous différentes solutions positives à cette même équation.
 Suite d'Or Parfaite
Suite d'Or Parfaite
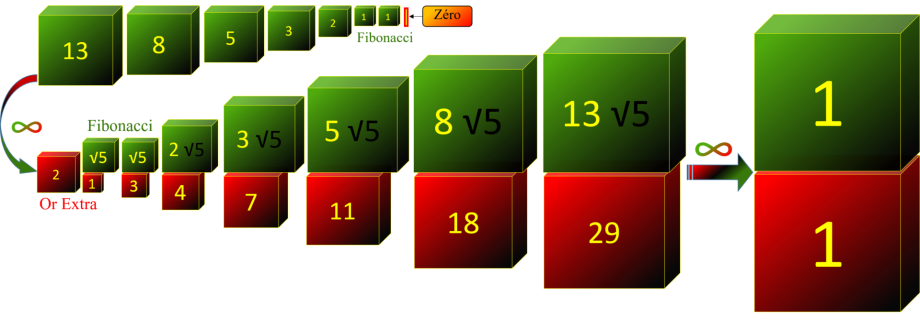
La suite d'Or Parfaite, est une suite de nombres irrationnels, qui
commence par l'unique nombre entiers le 2, suivi par une série de sommes entre nombres irrationnels (Fibonacci)×(√5) et nombres entiers (Or Extra).
Cette suite tend vers un nombre pair, car les termes (Fibonacci)×(√5), deviennent égales aux termes de
la suite Or Extra. Ce qui signifie que les nombres irrationnels (Fibonacci)×(√5) deviennent égales aux nombres entiers (Or Extra).
Rappelons la définition d'un nombre irrationnel : il ne peut s'écrire sous la forme d'une
fraction  avec (a) et (b) deux
nombres entiers. Or en considérant (a) comme terme de la suite Or Extra et (b) comme terme de la suite de Fibonacci, cette fraction
avec (a) et (b) deux
nombres entiers. Or en considérant (a) comme terme de la suite Or Extra et (b) comme terme de la suite de Fibonacci, cette fraction  se rapproche très rapidement
de la valeur de √5, qui est un nombre irrationnel.
se rapproche très rapidement
de la valeur de √5, qui est un nombre irrationnel.
La Suite d'Or Parfaite forme une boucle sans fin, allant d'un nombre pair à un autres nombre pair plus
grand.
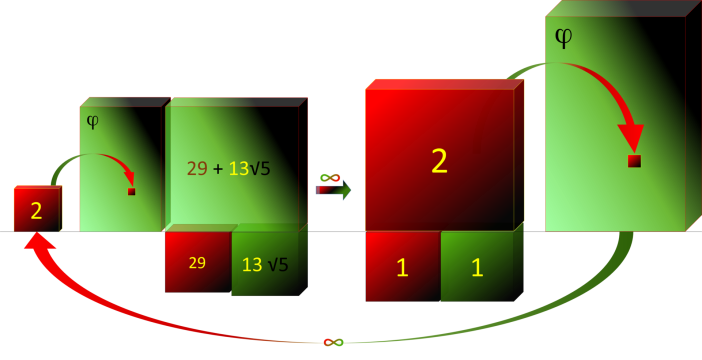 Boucle d'Or
Boucle d'Or
En suivant cette boucle en sens inverse, on s'aperçoit qu'il est impossible de retrouver le Rectangle de
Fibonacci du départ contenant le zéro. Car la boucle ne peut commencer qu'avec le chiffre 2. Ce qui n'est possible qu'avec la suite Or Extra.
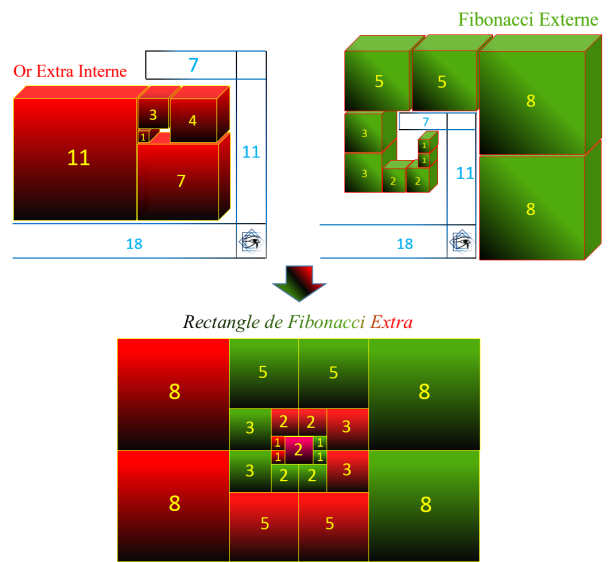
Ce Rectangle d'Or Extra, n'intègre pas le carré du départ correspondant au chiffre 2. Car il est
l'équivalent du Rectangle d'Horus, il correspond à la spirale interne.
Le Rectangle de Fibonacci Extra, correspond à la boucle de base du calcul d'Or Extra. Cette boucle commence
par l'unité 2, qui ne peut pas être divisée contrairement à tout les autres nombres qui sont présents en double.
L'unité 2, est l'équivalent de 1 (unité 1) de la boucle de base indo-arabe vue au premier chapitre. A
la différence près qu'ici le couple est celui du deuxième chapitre, le couple (OrExtra,Fibonacci).
Sachant que pour une opération d'addition, la boucle supérieure est un multiple de 5. Il suffit de
multiplier par 5 le Rectangle de Fibonnaci pour obtenir la boucle supérieure.
Sans surprise, ce Rectangle d'Or Extra commence par deux fois l'unité 2, l'équivalent de 2x5=10
l'unité de la boucle supérieure indo-arabe (unité 5).
Pour une opération de multiplication, l'unité est un multiple de √5. Ce qui correspond à la
spirale interne cachée sous les diagonales des bicarrés de chacun des deux Rectangles Extra.
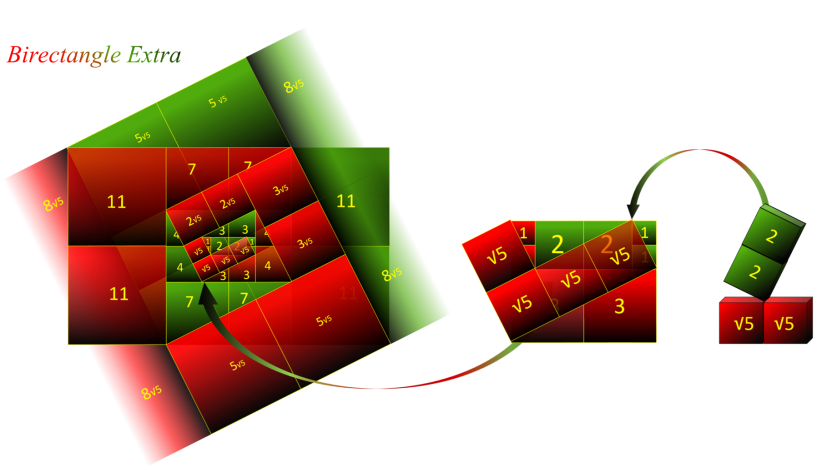
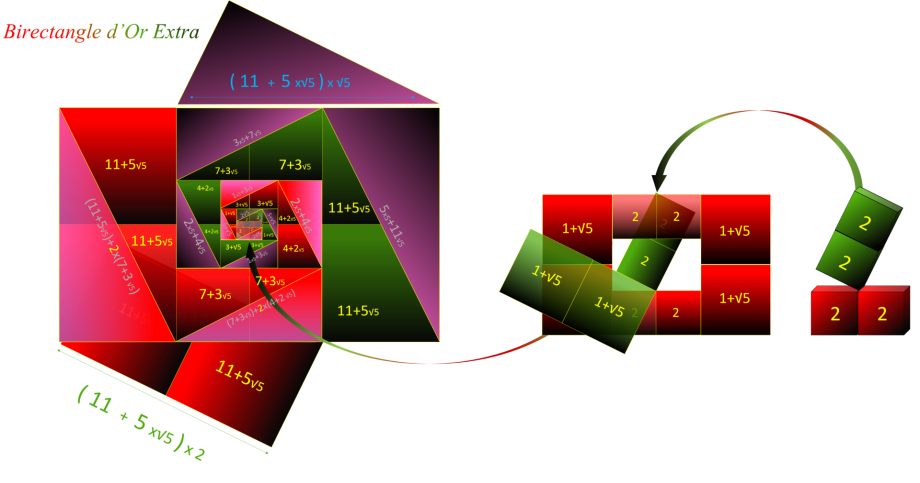
Ce Birectangle Extra tends vers le double du Rectangle d'Or Parfait :
La représentation géométrique du Birectangle d'Or Extra, montre que la diagonale de chaque bicarré est
égale à la longueur de son carré additionnée à celle du bicarré précédent.
Toutes les diagonales cachées sous le Birectangle Extra, deviennent visibles à travers le Birectangle d'Or
Extra. Ce qui semble signifier que les nombres supposés êtres irrationnels (a√5) sont composés uniquement de nombres entiers (a+2b).
Même avec toutes ces nouvelles géométries vues à travers ce chapitre 3 du Calcul d'Or Extra, l'énigme
du nombre d'Or reste entière, car ce chapitre ne traite qu'un tiers de l'unité (Rectangle d'Horus). Il manque encore les deux tiers (Carré d'Horus) représentants la spirale externe
d'Horus.