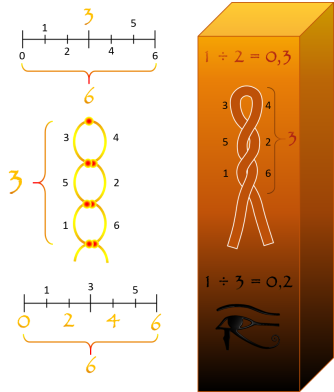Le système décimal
Ce sont justement les vérités les plus simples que l'homme découvre en dernier. (Ludwig Feuerbach)
Toutes les grandes découvertes scientifiques nous semblent évidentes à posteriori. Le concept de la virgule décimale qui nous est aujourd'hui si familier, fut une découverte d'une importance capitale que personne ne peut nier. Cependant il est difficile d'imaginer comment nos ancêtres ont pu s'en passer.
L'idée d'utiliser Les chiffres allant de 1 à 9 plus le symbole 0 pour représenter tous les nombres entiers de zéro à l'infini a d'abord été développé par des mathématiciens indiens aux environs du 6ième siècle. Mais l'idée d'utiliser un séparateur décimal fut révolutionnaire avec ce système numérique en permettant la représentation non seulement des nombres entiers mais aussi des fractions.
Aujourd'hui nos enfants sont initiés dès leur plus jeune âge aux chiffres indo-arabes, car c'est un langage
universel pratiqué par l'ensemble des scientifiques de notre monde actuel.
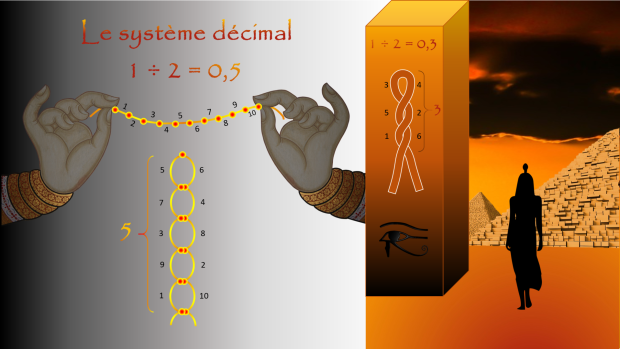
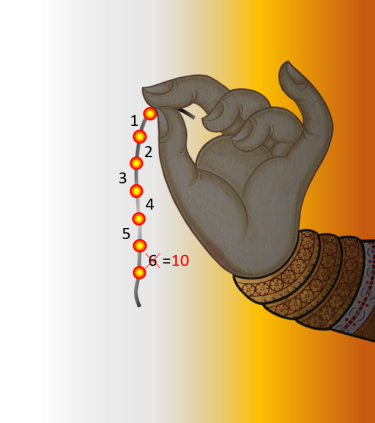
Pour compter de 1 à 10, il est nécessaire d'utiliser les chiffres allant de 1 à 9, puis le chiffre zéro qui est indispensable pour représenter le nombre 10. L'écriture du nombre 10 à l'aide du chiffre 1 suivi par le chiffre 0 signifie que le nombre 10 est égale à une fois la base, donc 1x10 pour un système décimal qui est à base de 10. Vu de cette manière cela ne vous évoque rien, car évidemment vous êtes habitués à ce système de numération qui prévoie que les chiffres s'arrêtent à 9.
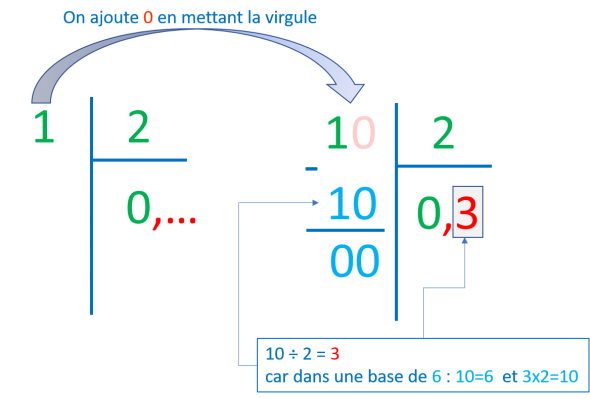
Si je vous dis que la moitié de 1 est égale à 0,3 ! Cela peut vous paraitre étrange, et pourtant vous avez l'habitude de dire que la moitié d'une heure est égale à 30 minutes, car l'unité qui est l'heure est constituée de 60 minutes dans un système de numération à base de 60. Or dans un système à base de 6, l'unité est constituée de 6, ce qui rend sa moitié égale à 0,3.
Tout comme dans un système à base de 10 les chiffres s'arrêtent à 9 , dans un système à base de 6 les chiffres devraient s'arrêter à 5 . Cela revient à considérer tous les chiffres allant de 6 à 9 comme inexistants. On peut donc dire que dans système à base de 6, les nombres s'écrivent (1,2,3,4,5,10,11,12,13,14,15,20,...), ce qui correspond à (1,2,3,4,5,6,7,8,9,10,11,12,...) dans notre système décimal habituel à base de 10. En effet dans une base de 6 le nombre 10 correspond à une fois la base donc 1x6, de même que le nombre 20 correspond à 2x6 ce qui vaut 12.
En réalité il n'y a aucune raison que les chiffres s'arrêtent à 9 ou à 5, car travailler dans un système de numération à base de 10 ou à base de 6 ne change en rien le résultat des calculs mathématiques enseignés par nos écoles. On a tendance à confondre l'invention du symbole zéro avec l'invention des chiffres, mais c'est uniquement l'invention du zéro qui a facilité toutes ces opérations mathématiques des calculs arithmétiques (soustraction, addition, division, multiplication), contrairement à l'invention prétendue des chiffres qui n'est en réalité qu'un accort mondial sur un langage universel.
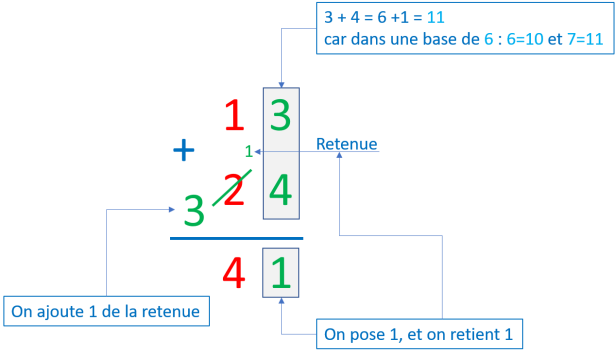
Si je vous dis que 13+24=41 ! vous vous dites que c'est faux. C'est pourtant une équation juste dans un système de numération à base de 6, mais le fait d'être habitué à travailler dans un système décimal programme votre cerveau à considérer ce genre d'égalité comme une aberration mathématique, et le but de ce cours est justement de vous libérer de cette programmation qui n'a aucun fondement scientifique.
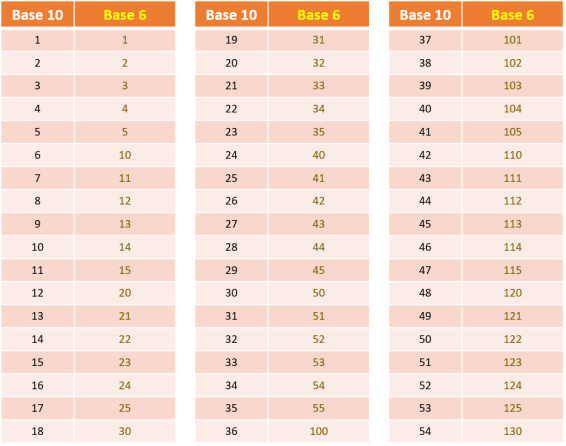
Pour mieux comprendre les calculs qui vont suivre, vous pouvez utiliser ce tableau pour le passage d'une numération à base de 10 à une numération à base de 6.
Il faut toujours garder à l'esprit que dans un système à base de 6, le chiffre 6 n'existe pas tout comme les chiffres 7, 8 et 9 n'existent pas non plus.
Ce tableau vous permettra de réaliser facilement des opérations mathématiques dans un système à base de 6 (système sénaire) tout en gardant une correspondance avec les nombres décimaux.
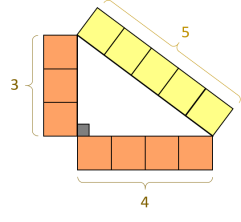
Cet exercice est très intéressant car nous avons ici un triangle avec des dimensions inférieures au chiffre 6, ce qui ne pose aucun problème pour travailler dans un système à base de 6. Mais en appliquant la formule de Pythagore nous allons vites arriver à des nombres supérieures à 6 en passant aux carrés des chiffres 3, 4 et 5.
Il y a trois règles à respecter pour passer d'un système décimal à un autre :
-
Le nombre 10 est égale à la base du système de numération étudié, ainsi 10=6 dans un système à base de 6.
-
Les chiffres s'arrêtent avant la base du système de numération étudié, ainsi les chiffres s'arrêtent à 5 dans un système à base de 6.
-
Quelque soit le système de numération étudié, les nombres s'écrivent toujours sous forme de multiple de la base additionnés à un chiffre du système étudié, ainsi dans une base de 6 le nombre 13 est un multiple de 6 (1x6) additionné à 3 ( 1x6+3=9 dans une base de 10).
Pas facile d'expliquer des choses aussi simples, mais vous allez vite vous y habituer en observant le calcul qui va suivre.
Pour retrouver les nombres décimaux de cette opération d'addition, il suffit d'écrire tous ces nombres sous forme de multiple de 6 additionné à un chiffre allant de 1 à 5 :
-
13 = 1 x 6 + 3 = 9
-
24 = 2 x 6 + 4 = 16
-
41 = 4 x 6 + 1 = 25
Ce qui montre que l'égalité 13 + 24 = 41 dans une base de 6, est la même que l'égalité 9 + 16 = 25 dans une base de 10, ce qui correspond à l'égalité obtenue à l'aide de la formule de Pythagore appliquée sur le triangle 3 4 5 avec 32+42=52.
Quelque soit le système de numération utilisé, tous ces calculs sont rendus possibles grâce au symbole 0 mais uniquement sur des nombres entiers. C'est pourquoi vous avez besoin de la virgule pour pouvoir calculer le résultat des fractions qui sont des nombres rationnels.
Souvenez-vous ! Dans un système de numération à base de 6 la moitié de l'unité est égale à 0,3 :
Vous vous demandez pourquoi faire compliqué quand on peut faire simple ?
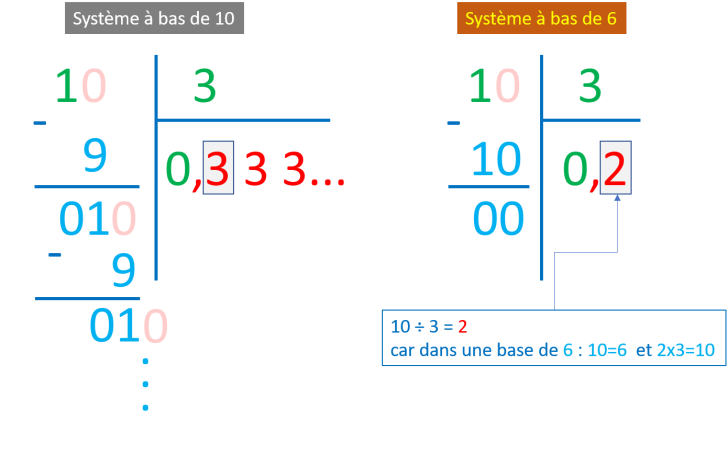
Détrompez-vous ! car si ce système à base de 6 peut vous paraitre compliqué, il peut s'avérer très utile pour simplifier certains calculs comme la division de 1 par 3 :
Dans un système de numération à base de 10 la division de l'unité par 3 exige la répétition sans fin du chiffre 3 après la virgule (0,333333....), ce qui n'est pas le cas avec un système de numération à base de 6 qui offre un résultat plus précis (0,2) surtout en cas de mesure de distance.
Vous vous êtes certainement rendu compte de l'importance du nombre 2 à travers le livre "Or Extra", ou tout simplement en lisant un article sur l'œil d'Horus égyptien, ou peut être en remarquant que l'équerre maçonnique contient des graduations divisées par deux, voir même en apprenant la langue arabe vous avez découvert la présence du duel en plus du singulier et du pluriel. Justement, tous les calculs vus précédemment vous ont permis de manipuler les nombres dans un système de numération à base de 6 qui est basé sur un nombre pair qui est le 6 (2x3=6) tout comme le système décimal est aussi basé sur un nombre pair qui est le 10 (2x5=10).
Ce pendant le système de numération à base de 6 nous a permis de calculer la division de 1 par 3 avec plus de précision en donnant un résultat égale à 0,2 car la base de 6 est un multiple de 3 contrairement à la base de 10 qui est un multiple de 5.